24 Вопрос.. Вынужденные колебания без учета сил сопротивления. Дифференциальное уравнение вынужденных колебаний и его интегрирование. Резонанс.

Рассмотрим движение материальной точки в том случае, когда на нее, кроме восстанавливающей силы F = −cOM , действует возмущающая сила P , периодически изменяющаяся с течением времени. Пусть проекция этой силы на ось х, вдоль которой совершается движение материальной точки, изменяется по гармоническому закону (рис.11). Px = Hsinpt (20) где Н – максимальное значение проекции силы Рх; р – частота возмущающей силы.

Составим дифференциальное уравнение точки, находящейся под действием указанных сил:

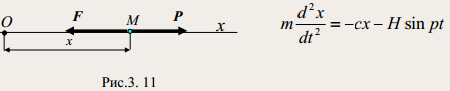
После преобразований: x``+ k2x = hsinpt (21)

В этом уравнении: k2 = c/m; h=H/m.

Общее решение неоднородного уравнения (21) равно х = х1 + х2, где x1 – общее решение соответствующего однородного дифференциального уравнения x``+ k2x=0,

а x2 –частное решение уравнения (21). Решение однородного уравнения x``+ k2x=0 запишем в виде: x1 = С1 sin kt + С2 coskt (22)

Частное решение x2 определяется в зависимости от соотношения частоты возмущающей силы p и частоты собственных колебаний k. Пусть частота возмущающей силы не равна частоте собственных колебаний. Для значений p ≠ k частное решение дифференциального уравнения (21) в соответствии с видом функции, стоящей в правой его части уравнения, следует искать в форме x2 = Asin ( pt +γ ) (23)

Уравнение (23) описывает гармонические колебания с частотой, равной частоте возмущающей силы.

Колебания материальной точки, происходящие с частотой возмущающей силы, называются вынужденными. А – амплитуда вынужденных колебаний; γ - начальная фаза.

Определим постоянные А и γ. Найдем вторую производную по времени от х2:

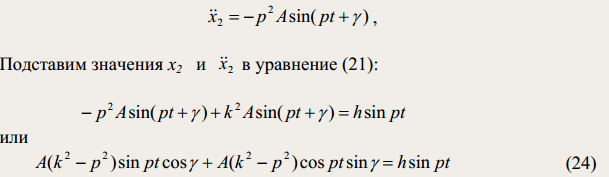
Полученное равенство справедливо при любом t, что возможно при равных коэффициентах, стоящих при одинаковых тригонометрических функциях в правой и левой его частях:

A(k2 – p2 ) cosγ = h (25)

A( k2 – p2)sin γ =0 (26)

Из уравнения (26) следует, что sin γ = 0, этому равенству удовлетворяют два значения начальной фазы: γ = 0, γ = π . Учитывая равенство (25), заключаем, что γ = 0 при условии, что р < k . В этом случае вынужденные колебания совпадают по фазе с возмущающей силой. Для колебаний, происходящих с частотой р > k, фаза вынужденных колебаний отличается от фазы возмущающей силы на величину π.

Таким образом, в случае вынужденных колебаний малой частоты точка всегда отклонена от начала координат в ту же сторону, куда в данный момент направлена возмущающая сила. В случае вынужденных колебаний большой частоты в любой момент времени отклонение точки от начала отсчета противоположно направлению возмущающей силы.

Из уравнения (25) получаем значение для амплитуды вынужденных колебаний (27)

Следовательно, уравнение вынужденных колебаний для р < k и для р > k, может быть записано в виде x2 =( h/k2 – p2) *sin pt. (28)

Подставим значение x1 = C1 sin kt + C2 cos kt и x2 =( h/k2 – p2) *sin pt в общее решение

x = x1+x2 уравнения (3.21): x = C1 sin kt + C2 cos kt + (h/k2 – p2)*sin pt (29)

Определим в уравнении (3.29) постоянные интегрирования С1 и С2. Для этого вычислим производную x`` = C1 k cos kt – C2k sin kt + (hp/k2 – p2) *cos pt (30) и подставим в выражение (3.29) и (3.30) начальные условия t = 0, x = x0, x` =x`0: x0 = C2, x`0 = C1k + (hp/ k2 – p2),

Откуда C1 = `x0/k – p/k*h/k2-p2, C2 = x0.

Уравнение движения точки (29) принимает вид

x= x0coskt + x0/k sinkt – p/k*h/k2-p2*sinkt + h/k2-p2*sin pt (31)

Движение точки является результатом трех движений:

1. свободных колебаний, возникающих под действием на точку восстанавливающей силы при начальных условиях x = x0, x` = x`0 и не зависящих от возмущающей силы: