24. Изоклины мультипликативной производственной функции.
Изоклинами наз-ся линии на плоскости KOL наиболее быстрого роста пр-ной ф-ции. Изоклины ортогональны линиям нулевого роста, т.е. ортогональны изоквантам. Поскольку направления наиболее быстрого роста в каждой точке (K, L) задается градиентом
,
то уравнение изоклины можно записать
следующим образом:
В частности для степенной мультипликативной производственной функции имеем: dF Y dF 0 Y, а тогда изоклину можно задать уравнением —KdK = — LdL, которое имеет решение К = + а), где а = К20~L\ = const.
Здесь К0 и L0 - координаты точки, через которую проходит изоклина. Если предположить, а = 0, то получим что изоклина представляет собой прямую линию К = L , проходящею через начало координат с коэффициентом наклона прямой дК dL
25. Коэффициент эластичности производственной функции
Важными хар-ми производ.ф-ии явл. коэф. эластич. выпуска по ресурсам.
ЕК
= -
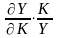ЕL
= -
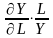Т.е. они равняются отношению предельной
производительности соответ. рес-са к
его сред.производ-ти.
Коэф. эластич. показывает на сколько % изменится выпуск прод-ции при увеличении затрат одного рес-са на 1 % и сохранении зн-я др.рес-са.
На ряду с
понятием эластич.выпуска
по затратам рес-сов
в эк.анализе применяется понятие
эластич. взаимозаменяемости
рес-сов. При
дв-нии вдоль изокванты F(K,L)=Y0
=const
вместе с координатами (.) (K,L) изменяется
зн-е
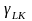, и велечина отношения затрат L/K.
Считая,что они связаны функционально:
L/K=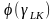
,
в предположении,что ф-я дифф-мая,вычислим
эластчность:
.
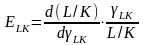Коэф. эластич. взаимозаменяемости
рес-сов ЕLK
показыв. на сколько % должно измениться
отношение затрат рес-сов,чтобы предельная
норма заменяемости рес-сов увелич. на
1%.
ЕLK
принимает
самые различные зн-я на промежутке
[0;
).
Чем выше зн-е коэф. эластич.взаимозамен.рес-сов,тем
в более широких пределах рес-сы могут
заменять др.др. При ЕLK
=0 возможность
замены рес-сов-отсутствует.При ЕLK
→
рес-сы могут заменять др.в самых широких
пределах.
26. Определение масштаба и эффективности строительства с помощью производственной функции.
Анализируя рес-сы,обеспечив.рост эк-ки выделяют: 1)- интенсивный (обеспечив.рост прод-та за счет увелич.эфф-ти использования рес-сов); 2)- экстенсивный (..за счет увелич. объемов затрат рес-сов).
С помощью производ.ф-ии можно выяснить масштабы использ.рес-сов. Только если выражено в соизмеримых ед.: -стоимостных;- относительных.
Рассмотрим мультипликат-ю производ.ф-ию,кот. будет в безразмероной форме.
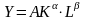- размерная
форма.
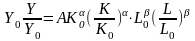или
,
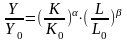тк.
.
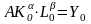Здесь Y0,K0,L0
– зн-я объема
выпуска продукции,затрат фондов и труда
в базовом году. Если использовать
выпуск.продукцию и рес-сы в безразмерн.форме
и обозначить их соответств.ч/з
,
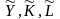то мультипликат.производ.ф-я может быть
записана в ви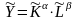де:
,
где
.
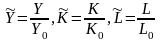Под эфф-тью
пр-ва – поним.
отношение результат пр-ва к затратам
рес-са.В рассмотр. модели Кобба-Дугл.учитыв.
два вида затрат: 1)затраты прошедшего
труда (фонды, капитал)
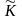;2)
затраты живого труда
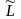.Соответ.будет
два частных показателя эфф-ти
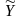/К-
фондоотдача;
/L-
продуктивность.
Т.к. приведенные частные показатели эфф-ти безразмерны,то можно ввести средн.зн-е эфф-ти:
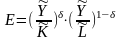( сред.геом.взвешенный
частный показатель).
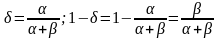-относит эл-ти, играющие роль весовых
коэф.
Из выражения для показателя эффективности следует, что с помощью коэффициента экономической эффективности производственную функцию можно представить в форме, которая по внешнему виду совпадает с функцией Кобба – ДугласаY = EKaL'-a.
Отличие заключается в том, что в представленной форме показатель эффективности Е не является постоянным коэффициентом, а является функцией от ресурсов К и L.
27. Построение балансовой модели.
28.Продуктивные модели Леонтьева.
29.Модель равновесных цен.
30.Модель международной торговли (модель обмена).
31.Модель стабилизации цены на рынке одного товара (модель Эванса).
32.Модель предприятия.