7.Функция спроса по цене.

Спрос - платежеспособная потребность покупателя, т.е. потребность покупателя, располаг ден ср-ми для приобретения товаров и услуг.

Под потребностью понимается нужда человека в конкретных благах, необх для поддержания жизнедеятельности и развития личности.

На спрос влияет 3 фактора: потребность человека в продукте; цена; уровень ден дохода потребителя.

В основе рыночного спроса лежит правило убывающей предельной полезности: «чем выше цена, тем меньше тех, кто согласится купить данный товар, т.е. меньше уровень спроса и наоборот». Напр чем меньше цена жд билета тем больше спрос на него при пост покуп-й способности населения.

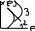
График денежного спроса имеет вид убывающей кривой, а ее аналитическое выражение х(р)=с₀р^альфа+с₁. Для кривой 1 – C0>0,C1>0,α<0, p (цена)>0, x(спрос) >0

На значения коэффициентов С0 и С1 оказывает влияние число потребителей на рынке, ден доходы и вкусы потребителей, цены конкурентов и цены на замещающие товары и др.

Для прямой 2 - C1>0, C0<0, α=1

Для кривой 3 - C1>0, C0<0,α>0

Общим св-ом для всех кривых явл отриц знач производной p’(x). Обуславл для 1 кривой α<0, для ост C0<0.

8. Построение функции спроса методом наименьших квадратов.

9. Построение функции предложения методом наименьших квадратов.

(2 в 1)

В качестве исходных данных для построения ф-ии спроса и предложения выступают данные n незав набл за спросом (предлож) и соотв ему цене.

Эти набл можно представить в виде вектор столбца Х и У. эл-ты столбца х выступ в кач-ве знач цены, фиксируемой в iом опыте. Вектор столбец у сост из компонент представл собой знач спроса (предлож), фиксируемых в каждом iом опыте.

Ф-и спр и предл м.б. как лин, так и нелин. В случ лин ф-и она им вид: у_х=а+bx. Хар-ет семейства прямых, каждое из которых характеризуется конкретными значениями коэффициентов а и Ь, Наилучшей из всего множества прямых для рассматриваемой выборки является та прямая, которая на плоскости хОу расположена "ближе" всего, в определенном смысле, к опытным точкам. В качестве меры близости прямой и некоторой точки на плоскости можно выбрать расстояние между ними. При этом под расстоянием следует понимать модуль разности между опытным (наблюдаемым) значением результирующей величины и теоретическим.

В качестве критерия близости между прямой и множеством точек на плоскости целесообразно выбрать минимум суммы квадратов этих расстояний. Е=∑(yi-a-bx_i)^2->min. Здесь считается, что y_t и x_i - известные статистические данные; а

и Ъ — неизвестные параметры (коэффициенты) функции регрессии. Поскольку функция Е непрерывна, выпукла и ограничена снизу нулем, то она имеет минимум. Изложенная идея минимизации суммы квадратов отклонений (на плоскости расстояний) опытных от теоретических значений объясняемой переменной положена в основу метода наименьших квадратов.

Если необходимо оценить коэфф-ты линейной ф-ии спроса, то применяют непосредственно метод наименьших квадратов p(x)=Co+C1(x). Если нелинейная ф-ия – используют линеаризацию. Самостоятельно применяют метод наим. кВ. для нелинейной ф-ии спроса, т.е. линеаризируют функцию зависящую .
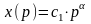