Формулы приведения

Формулы сложения тригонометрических функций

1. sin (α + β) = sin α · cos β + sin β · cos α

2. sin (α - β) = sin α · cos β - sin β · cos α

3. cos (α + β) = cos α · cos β - sin α · sin β

4. cos (α - β) = cos α · cos β + sin α · sin β

5. tg (α + β) = (tg α + tg β) ÷ (1 - tg α · tg β)

6. tg (α - β) = (tg α - tg β) ÷ (1 + tg α · tg β)

7. ctg (α + β) = (ctg α · ctg β + 1) ÷ (ctg β - ctg α)

8. ctg (α - β) = (ctg α · ctg β - 1) ÷ (ctg β + ctg α)

Формулы для половиннных углов

Для любого угла α справедливы равенства:

cos2α/2 = (1 + cos α)/2

sin2α/2 = (1 – cos α)/2

Для любого угла α такого, что α ≠ π + 2πk (k принадлежит множеству Z), справедливо:

tg2α/2 = (1 – cos α)/(1 + cos α)

ctg2α/2 = (1 + cos α)/(1 – cos α)

tg α/2 = sin α/(1 + cos α)

cos α = (1 – tg2α/2)/(1 + tg2α/2)

sin α = (2 tg α/2)/(1 + tg2α/2)

Для любого угла α такого, что α ≠ πk (k принадлежит множеству Z), справедливо:

tg α/2 = (1 – cos α)/(sin α)

ctg α = (1 – tg2α/2)/(2 tg α/2)

Для любого угла α такого, что α ≠ π + 2πk и α ≠ π/2 + πn (k, n принадлежат множеству Z), справедливо:

tg α = (2 tg α/2)/(1 – tg2α/2)

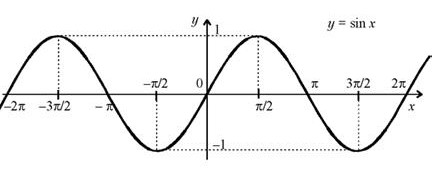
функции y=sinx и основные свойства и графики

а)  Область определения:   D (sin x) = R .

    б)  Множество значений:   E (sin x) = [ – 1 ,  1 ] . в)  Четность, нечетность:   функция нечетная.

    г)  Периодичность:   функция периодическая с основным периодом 

T = 2 .

    д)  Нули функции:  sin x = 0  при   x =  n,   n   Z.

    е)  Промежутки знака постоянства:

;       .

      ж)  Промежутки монотонности: ;

.

      з)  Экстремумы:  ;           .

     График функции    y= sin x   изображен на рисунке.

   функции y= cos x 

а)  Область определения:   D (cos x) = R .

    б)  Множество значений:   E (cos x ) = [ – 1 ,  1 ] . в)  Четность, нечетность:   функция четная.

    г)  Периодичность:   функция периодическая с основным периодом 

T = 2 .

    д)  Нули функции:  cos x = 0  при   x =   +  n,   n   Z.

   е)  Промежутки знака постоянства:

;   .

.      ж)  Промежутки монотонности:

;

.

      з)  Экстремумы:

;             .

     График функции    y= cos x   изображен на рисунке.

функции y=tg  x 

а)  Область определения:   D (tg x) = R \ { /2 +   n( n   Z ) }.

    б)  Множество значений:   E (tg x ) = R . в)  Четность, нечетность:   функция нечетная.

    г)  Периодичность:   функция периодическая с основным периодом

  T =  .

    д)  Нули функции:  tg x = 0  при   x =  n,   n   Z.

      е)  Промежутки знакопостоянства:

;        .

      ж)  Промежутки монотонности:  функция возрастает на каждом интервале, целиком принадлежащем ее области определения.

      з)  Экстремумы:  нет.

   График функции   y = tg x   изображен на рисунке.

функции y=ctg  x 

а)  Область определения:   D (ctg x) = R \ {  n( n   Z ) }.

    б)  Множество значений:   E (ctg x ) = R . в)  Четность, нечетность:   функция нечетная.

    г)  Периодичность:   функция периодическая с основным периодом  T =  .

    д)  Нули функции:  ctg x = 0  при   x =  /2 +  n,   n   Z.

    е)  Промежутки знакопостоянства ; ;        .

     ж)  Промежутки монотонности:  функция убывает на каждом интервале, целиком принадлежащем ее области  определения.

     з)  Экстремумы:  нет.

   График функции   y = ctg x  изображен на рисунке.

 

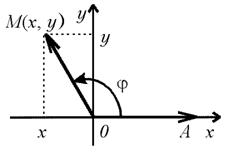
Определение функции.

пусть    –  угол между подвижным радиус-вектором  OM= { x, y}  и его начальным  положением  OA.

     а) Синусом  угла      называется отношение ординаты  y  конца подвижного  радиус-вектора  r = OM   к  длине   r = | r  | этого радиус-вектора, т.е.   б)  Косинусом угла    называется отношение абсциссы  x  конца подвижного радиус-вектора  r = OM   к длине   r = | r  |  этого радиус-вектора, т.е.

     в)  Тангенсом угла   называется отношение ординаты  y  к абсциссе  x конца подвижного радиус-вектора   OM .  т.е. 

     г)  Котангенсом   угла     называется отношение абсциссы  x  к ординате  y  конца подвижного радиус-вектора    OM ,  т.е.  

      д) Функции  секанс  и  косеканс определяются соотношениями

     Подчеркнем, что отношения

зависят только от величины  угла      и не зависят от длины  r  радиус-вектора OM.  Это означает,  что тригонометрические функции 

являются функциями только угла   .  При этом угол     часто называют аргументом тригонометрических функций. При вычислении тригонометрических функций можно пользоваться подвижными  радиус-векторами длины  r = 1.   Концы таких векторов лежат на единичной окружности    .   В этом случае

Область определения - это значения "Х"

(т.е. какие значения может принимать Х) А область значения - это "у" (т.е. какие "у" при этом получаются)

 

4 способа задания функции: