Определение скалярного произведения векторов. Скалярным произведением двух векторов называется действительное число, равное произведению длин умножаемых векторов на косинус угла между ними.

Скалярное произведение векторов   и   будем обозначать как  . Тогда формула для вычисления скалярного произведения имеет вид  , где   и  - длины векторов   и   соответственно, а   - угол между векторами   и  .

Из определения скалярного произведения видно, что если хотя бы один из умножаемых векторов нулевой, то  .

Вектор можно скалярно умножить на себя. Скалярное произведение вектора на себя равно квадрату его длины, так как по определению  Скалярное произведение вектора на себя называется скалярным квадратом.

Формулу для вычисления скалярного произведения   можно записать в виде  , где   - числовая проекция вектора   на направление вектора  , а   - числовая проекция вектора   на направление вектора  .

Таким образом, можно дать еще одно определение скалярного произведения двух векторов.

Скалярным произведением двух векторов   и   называется произведение длины вектора   на числовую проекцию вектора   на направление вектора   или произведение длины вектора   на числовую проекцию вектора   на направление вектора  .

Расстояние между двумя точками на плоскости расчитывается по следующей формуле:

где x₁ и y₁ координаты первой точки, а x₂ и y₂ координаты второй точки.

Расстояние между двумя точками в трехмерном пространстве рассчитывается по следующей формуле:

где x₁, y₁ и z₁ координаты первой точки, а x₂, y₂ и z₂ координаты второй точки.

Расстояние между точками в пространстве 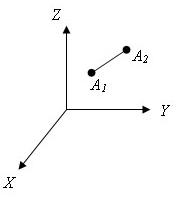  Есть две произвольные точки A1(x1;y1;z1) и A2(x2;y2;z2)  Тогда расстояние между точками A1 и A2 вычисляется так: 

Углы, получающиеся при непрерывном вращении, удобно измерять не в градусах, а с помощью таких чисел, которые отражали бы сам процесс построения угла, т.е. вращение.  Для описания непрерывного вращения градусная мера угла поворота становится неудобной – с ней трудно связывать другие характеристики движения, например, скорость или соединять вращательное движение с иными движениями. Поэтому вводят другую меру угла поворота, так называемую радианную меру.

При малых углах синус и тангенс угла, выраженного в радианах, приблизительно равны самому углу, что удобно при приближённых вычислениях:

Синусом α называется отношение AB/OB (противолежащего катета к гипотенузе)  Косинусом α называется отношение ОА/OB (прилежащего катета к гипотенузе)  Тангенсом α называется отношение AB/OA (отношение противолежащего катета к прилежащему)  Котангенсом α называется отношение ОА/AB (отношение прилежащего катета к противолежащему)  Секансом α называется отношение ОB/OA (гипотенузы к прилежащему катету)  Косекансом α называется отношение ОB/AB (гипотенузы к противолежащему катету) .

ЗНАКИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ПО ЧЕТВЕРТЯМ В ТРИГОНОМЕТРИЧЕСКОМ КРУГЕ
Функция / четверть	I	II	III	IV
sin α	+	+	–	–
cos α	+	–	–	+
tg α	+	–	+	–
ctg α	+	–	+	–