Перпендикулярные прямые

Прямая (отрезок прямой) обозначается двумя большими буквами латинского алфавита или одной маленькой буквой. Точка обозначается только большой латинской буквой.

Прямые могут не пересекаться, пересекаться или совпадать. Пересекающиеся прямые имеют только одну общую точку, непересекающиеся прямые — ни одной общей точки, у совпадающих прямых все точки общие.

Определение. Две прямые, пересекающиеся под прямым углом, называются перпендикулярными. Перпендикулярность прямых (или их отрезков) обозначают знаком перпендикулярности «⊥».

Например:

Ваш AB и CD (рис. 1) пересекаются в точке О и ∠АОС = ∠ВОС = ∠АОD = ∠BOD= 90°, то AB ⊥ CD.

Если AB ⊥ CD (рис. 2) и пересекаются в точке В, то ∠АBC = ∠ABD = 90°

Свойства перпендикулярных прямых

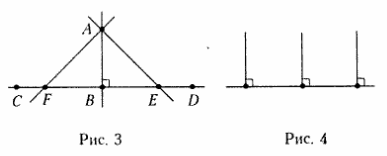
1. Через точку А (рис. 3) можно провести только одну перпендикулярную прямую АВк прямой СD; остальные прямые, проходящие через точку А и пересекающие СD, называются наклонными прямыми (рис. 3, прямые АЕ и АF).

2. Из точки A можно опустить перпендикуляр на прямую CD; длина перпендикуляра (длина отрезка АВ), проведенного из точки А на прямую CD,— это самое короткое расстояние от A до CD (рис. 3).

3. Несколько перпендикуляров, проведенных через точки прямой к прямой, никогда между собой не пересекаются (рис. 4).

Пусть прямая пересекает плоскость, причем не под прямым, а под каким-то другим углом. Такая прямая называется наклонной.

Опустим перпендикуляр из какой-либо точки наклонной на нашу плоскость. Соединим основание перпендикуляра с точкой пересечения наклонной и плоскости. Мы получили проекцию наклонной на плоскость.

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.

Если прямая параллельна плоскости, значит, угол между прямой и плоскостью равен нулю.

Если прямая перпендикулярна плоскости, ее проекцией на плоскость окажется точка. Очевидно, в этом случае угол между прямой и плоскостью равен 90°.

Прямая перпендикулярна плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.

Размещениями из n различных элементов по m элементов (m ≤ n) называются комбинации, составленные из данных n элементов по m  элементов и отличающиеся либо самими  элементами, либо порядком элементов.  

Например, из трех элементов a, b, c можно составить следующие размещения по два  элемента:   . Число различных размещений из n элементов по m элементов (обозначение:  ) определяется по формуле  .  

Перестановками из n различных элементов называются размещения их этих n элементов по n.  

Как видно из определений, перестановки можно считать частным случаем размещений при m = n.  Следовательно, число всех  перестановок из n элементов (обозначение:  ) находится по формуле    Сочетаниями из n различных элементов по m элементов называются комбинации, составленные из данных n элементов по m элементов и  отличающиеся хотя бы одним элементом.  

Отметим разницу между сочетаниями и  размещениями: в сочетаниях не учитывается порядок элементов, а в размещениях — учитывается. Число сочетаний из n элементов по m элементов (обозначение:   , иногда  ) находится по формуле   

Свойства сочетаний.

1.   

2.   

3.  4.   

Формула бинома Ньютона 

     Если k-й член ((k+1)-е слагаемое) разложения степени бинома обозначать через  , то

-1-2-

Правила комбинаторики

1) Число перестановок из n элементов находится по формуле:

2) Число размещений из n элементов по m находится по формуле:

3) Число сочетаний из n элементов по m находится по формуле:

4) Справедливы следующие свойства сочетаний:

Прямоугольная система координат на плоскости

Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X’X и Y’Y. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление.Положительное направление осей (в правосторонней системе координат) выбирают так, чтобы при повороте оси X’X против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси Y’Y. Четыре угла (I, II, III, IV), образованные осями координат X’X и Y’Y, называются координатными углами (см. Рис. 1).

Рис. 1

Положение точки A на плоскости определяется двумя координатами x и y. Координата x равна длине отрезка OB, координата y — длине отрезка OC в выбранных единицах измерения. Отрезки OB и OC определяются линиями, проведёнными из точки A параллельно осям Y’Y и X’X соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A. Записывают так: A(x, y).

Если точка A лежит в координатном угле I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном угле II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном угле III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном угле IV, то точка A имеет положительную абсциссу и отрицательную ординату.

Вектор – это направленный отрезок прямой.

То есть, в качестве вектора мы принимаем отрезок на плоскости или в пространстве, считая одну из его граничных точек началом, другую – концом.

Для обозначения векторов будем использовать строчные латинские буквы со стрелочкой над ними, например  . Если заданы граничные точки начала и конца отрезка, к примеру А и В, то вектор будем обозначать как  .

Нулевой вектор   – это любая точка плоскости или пространства.

Будем считать, что нулевому вектору можно придать любое направление на плоскости и в пространстве.

Длина вектора   - это неотрицательное число, равное длине отрезка АВ.

Длину вектора   будем обозначать как  .

Так как обозначение длины вектора в точности совпадает со знаком модуля, то можно услышать, что длину вектора называют модулем вектора. Все же рекомендуем использовать термин "длина вектора". Длина нулевого вектора равна нулю.

Два вектора называют коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых.

Два вектора называют неколлинеарными, если они не лежат на одной прямой или параллельных прямых.

Нулевой вектор коллинеарен любому другому вектору.

Два коллинеарных вектора   и   называют сонаправленными, если их направления совпадают и обозначают  .

Определение.

Два коллинеарных вектора   и   называют противоположно направленными, если их направления противоположны и обозначают  ).

Будем считать, что нулевой вектор сонаправлен с любым другим вектором.

Два вектора называются равными, если они сонаправленные и их длины равны.

Два вектора называются противоположными, если они противоположно направлены и их длины равны.

Понятие равных векторов дает нам возможность рассматривать векторы без привязки к конкретным точкам. Другими словами, мы имеем возможность заменить вектор равным ему вектором, отложенным от любой точки.

Пусть   и   два произвольных вектора на плоскости или в пространстве. Отложим от некоторой точки O плоскости или

пространства векторы   и  .

Лучи OA и OB образуют угол  .

Угол   называется углом между векторами   и  .

Угол между сонаправленными векторами равен нулю градусам (или нулю радиан), а угол между противоположно направленными векторами

равен 180 градусам (или   радиан).

Два вектора называются перпендикулярными, если угол между ними равен 90градусам (или   радиан).

Уравнение окружности ω (A; R) имеет вид (x – a)² + (y – b)² = R², где a и b – координаты центра A окружности ω (A; R) .

Доказательство

Пусть задана окружность ω (A; R) на плоскости Оху, где точка A, центр окружности – имеет координаты a и b. По определению окружности для любой точки B (x; y), лежащей на окружности ω (A; R), верно AB = R. Но в соответствии с теоремой  AB2 = (x – a)2 + (y – b)2. Таким образом, координаты x и y любой точки окружности ω (A; R) удовлетворяют уравнению (x – a)2 + (y – b)2 = R2. Обратно: любая точка B (x; y), координаты которой удовлетворяют уравнению, принадлежит окружности, так как расстояние от нее до точки A (a; b) равно R. Отсюда по определению данное уравнение – уравнение окружности ω (A; R). Уравнение окружности с центром в начале координат: x2 + y2 = R2

Кривой 2–го порядка называется линия на плоскости, которая в некоторой декартовой системе координат определяется уравнением

ax2 + 2bxy + cy2 + 2dx + 2ey + f = 0,

Прямые x, y, z называются координатными осями (или осями

координат),  точка их пересечения O – началом координат,  а плоскости xOy, xOz и yOz – координатными плоскостями.  Точка O разбивает каждую координатную ось на две полупрямые, которые называются положительной и отрицательной полуосями.

Координатой точки A по оси x будем называть число, равное по абсолютной величине длине отрезка OA_x: положительное, если точка A лежит на положительной полуоси x, и отрицательное, если она лежит на отрицательной полуоси.

Аналогично можно определить координаты y и z точки A. Координаты точки A записываются в скобках рядом с названием этой точки: A (x; y; z).

Единичным вектором или ортом называется вектор, длина которого равна единице и который направлен вдоль какой-либо координатной оси.

• Единичный вектор, направленный вдоль оси x, обозначается i .

• Единичный вектор, направленный вдоль оси y, обозначается j .

• Единичный вектор, направленный вдоль оси z, обозначается k .

Вектора i , j , k  называются координатными векторами.

• Любой вектор a  можно разложить по координатным векторам: a =x i +y j +z k.

Коэффициенты разложения определяются единственным образом и

Свойства векторов, заданных координатами

• Координаты нулевого вектора равны нулю.

• Координаты равных векторов соответственно равны.

• Координаты вектора суммы двух векторов равны сумме соответствующих координат этих векторов.

• Координаты вектора разности двух векторов равны разностям соответствующих координат этих векторов.

• Координаты вектора произведения данного вектора на число равны произведениям соответствующих координат этого вектора на данное число