Натуральные числа – это числа, получаемые при естественном счёте предметов, а вернее при их нумерации («первый», «второй», «третий»...). Множество натуральных чисел обозначается латинской буквой  Можно сказать, что N ={1,2,3,....}Целые числа – это числа из множества {0, 1, -1, 2, -2, ....}. Это множество состоит из трех частей – натуральные числа, отрицательные целые числа (противоположные натуральным числам) и число 0 (нуль). Целые числа обозначаются латинской буквой Z. Можно сказать, чтоZ={1,2,3,....}.Рациональные числа – это числа,представимые в виде дроби , где m — целое число, а n — натуральное число. Для обозначения рациональных чисел используется латинская буква Q. Все натуральные и целые числа – рациональные. Также в качестве примеров рациональных чисел можно привести:  , , .Действительные (вещественные) числа – это числа, которое применяются для измерения непрерывных величин. Множество действительных чисел обозначается латинской буквой  R. Действительные числа включают в себя рациональные числа и иррациональные числа. Иррациональные числа – это числа, которые получаются в результате выполнения различных операций с рациональными числами (например, извлечение корня, вычисление логарифмов), но при этом не являются рациональными. Примеры иррациональных чисел – это , , .Любое действительное число можно отобразить на числовой прямой:

Для перечисленных выше множеств чисел справедливо следующее высказывание: То есть множество натуральных чисел входит во множество целых чисел. Множество целых чисел входит во множество рациональных чисел. А множество рациональных чисел входит во множество действительных чисел. Это высказывание можно проиллюстрировать с помощью кругов Эйлера.

Абсолютная погрешностьНайдем по графику функции y = x² её приближенное значение при x = 1.5  если x = 1.5, то y ≈ 2.3.По формуле y = x² можно найти точное значение этой функции:  если x = 1.5, то y = 1.5² = 2.25  Приближенное значение отличается от точного на 0.05, так как 2.3 - 2.25 = 0.05.  Чтобы узнать, на сколько приближенное значение отличается от точного, надо из большего числа вычесть меньшее. Иначе говоря, надо найти модуль разности точного и приближенного значений. Этот модуль разности называют абсолютной погрешностью.  Определение: Абсолютной погрешностью приближенного значения называется модуль разности точного и приближенного значений.  Если x ≈ a и абсолютная погрешность этого этого приближенного значения не превосходит некоторого числа h, то числа a называют приближенным значением x с точностью до h.  Точность приближенного значения зависит от многих причин. В частности, если приближенное значение получено в процессе измерения, то точность зависит от прибора, с помощью которого выполнялось измерение.  Относительная погрешностьПри измерении (в сантиметрах) толщины b стекла и длины l книжной полки получили результаты:  b≈0.4 с точностью до 0.1  l≈100.0 с точностью до 0.1  Абсолютная погрешность каждого из этих измерений не превосходит 0.1. Однако 0.1 составляет существенную часть числа 0.4 и ничтожную часть числа 100. Это показывает, что качество второго измерения намного выше, чем первого. Для оценки качества измерений используется относительная погрешность приближенного значения.  Определение: относительной погрешностью приближенного значения называется отношение абсолютной погрешности к модулю приближенного значения. 

1)Комплексным числом называется выражение вида a + ib, где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей. Для таких выражений понятия равенства и операции сложения и умножения вводятся следующим образом:

1)Два комплексных числа a + ib и c + id называются равными тогда и только тогда, когда  a = c и b = d. 2)Суммой двух комплексных чисел a + ib и c + id называется комплексное число a + c + i(b + d). 3)Произведением двух комплексных чисел a + ib и c + id называется комплексное число ac – bd + i(ad + bc). Комплексные числа часто обозначают одной буквой, например, z = a + ib. Действительное число a называется действительной частью комплексного числа z, действительная часть обозначается a =Re z.Действительное число b называется мнимой частью комплексного числа z, мнимая часть обозначается b = Im z. В отличие от действительных чисел, числа вида 0 + ib называются чисто мнимыми.

Приближенные значения действительных чисел

. Но производить вычисления с бесконечными десятичными неудобно, поэтому на практике пользуются приближенными значениями действительных чисел. Например, для числа   пользуются приближенным равенством  3,141 или   3,142. Первое называют приближенным значением (или приближением) числа п по недостатку с точностью до 0,001; второе называют приближенным значением (приближением) числа к по избытку с точностью до 0,001. Определение. Погрешностью приближения (абсолютной погрешностью) называют модуль разности между точным значением величины х и ее приближенным значением а: погрешность приближения — это | х - а |. 

Степень с натуральным показателем-это число, полученное путем возведения основания степени в показатель степени, который является положительным целым числом.  Степень с целым показателем-это число, полученное путем возведения основания степени в показатель степени, который является просто целым числом (в том числе и отрицательным).

 1-ое свойство         При умножении степеней с одинаковыми основаниями         показатели складываются, а основание остается неизменным.        если a — любое число, а n и k — натуральные числа то:                     a n • a k   =   a ^N+K  

Степенной функцией с вещественным показателем a называется функция y = x ⁿ , x >0.Заметим, что для натуральных n степенная функция определена на всей числовой оси.  Для произвольных вещественных n это невозможно, поэтому степенная функция с вещественным показателем определена только для положительных x .

К основным свойствам степенной функции y = x ^a при a > 0 относятся:

Область определения функции - промежуток (0; +  ).

Область значений функции - промежуток (0; + ).

Для любых a график функции проходит через точку (1; 1).

Функция строго монотонно возрастает в области определения функции, то есть, если x₁ < x₂ то a^r₁ < a^r₂ .

График степенной функции при a > 0 изображен на рисунке.

К основным свойствам степенной функции y = x ^a при a < 0 относятся:

1.Область определения функции - промежуток (0; + ).

2.Область значений функции - промежуток (0; + ).

3.Для любых a график функции проходит через точку (1; 1).

4.Функция строго монотонно возрастает в области определения функции, то есть, если x₁ < x₂ то a^r₁ > a^r₂ .

5.

График степенной функции при a < 0 изображен на рисунке.

Справедливы следующие свойства степенной функции: 

• x^a₁x^a₂ = x^a₁ ^{+ a}₂

• x^a₁ : x^a₂ = x^a₁ ^{- a}₂

• (x^a₁)^a₂ = x^a₁ ^a₂

• x^a₁ > x^a₂, x > 1, a₁ > a₂

• x^a₁ < x^a₂, 0 < x < 1, a₁ < a₂

Степень с рациональным показателем

Пусть дано положительное число   и произвольное рациональное число  . Число  называется степенью, число   — основанием степени, число   — показателем степени.

По определению полагают:

.

.

, .

Е сли   — целое, а   — натуральное число и  , то 

Частные случаи:

.

.

.

.

Свойства степени с рациональным показателем

Если   и   — положительные числа,   и   — любые рациональные числа, то справедливы следующие свойства:

• .

• .

• .

• .

• .

• .

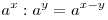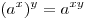Степень с действительным показателем

Пусть дано положительное число   и произвольное действительное число  . Число  называется степенью, число   — основанием степени, число   — показателем степени.

По определению полагают:

.

.

,  .Если   и   — положительные числа,   и   — любые действительные числа, то справедливы следующие свойства:

• .

• .

• .

• .

• .

• .

Логарифмом данного числа называется показатель степени, в которую нужно возвести другое число, называемое основанием логарифма, чтобы получить данное число.

 Логарифм по основанию 10, т. е. показатель степени, в которую надо возвести 10, чтобы получить это число. Д. л. числа N обозначается lgN; например lg100 = 2.

Основное логарифмическое тождество

Логарифм произведения — это сумма логарифмов

Логарифм частного — это разность логарифмов

Сложение и вычитание логарифмов

Рассмотрим два логарифма с одинаковыми основаниями: log_a x и log_a y. Тогда их можно складывать и вычитать, причем:

1. log_a x + log_a y = log_a (x · y);

2. log_a x − log_a y = log_a (x : y).

Аксиомы стереометрии

 А к с и о м а 1.Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

 А к с и о м а 2.Если две точки прямой лежат в плоскости, то все точки данной прямой лежат в этой плоскости.

В этом случае говорят, что прямая лежит в плоскости или что плоскость проходит через прямую.

Из аксиомы 2 следует, что прямая, не лежащая в плоскости, не может иметь с плоскостью более одной общей точки. Если прямая и плоскость имеют только одну общую точку, то говорят, что прямая пересекает плоскость.

 А к с и о м а 3.Если две плоскости имеют общую точку, то они имеют общую прямую, которой принадлежат все общие точки этих плоскостей.

В этом случае говорят, что плоскости пересекаются по прямой.

 А к с и о м а 4.В любой плоскости пространства выполняются все аксиомы планиметрии. Таким образом, в любой плоскости пространства можно использовать все доказанные теоремы и формулы из планиметрии.

Некоторые следствия из аксиом

 С л е д с т в и е 1.Через прямую и не лежащую на ней точку проходит плоскость и притом только одна.

 С л е д с т в и е 2.Через две пересекающиеся прямые проходит плоскость и притом только одна.

 С л е д с т в и е 3.Через две параллельные прямые проходит плоскость и притом только одна.

1)Взаимное расположение прямых в пространстве. Расположение прямой и плоскости пространства.  2) Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не имеют общих точек.  3)Если две прямые параллельны третей, то они параллельны между собой.  4)Если одна из двух параллельных прямых пересекает плоскость, то и вторая параллельная прямая пересекает эту плоскость  5)Через точку не лежащую на заданной прямой можно построить только одну параллельную к данной прямой.  6) Если прямые пересекаются, то они имеют только одну общую точку.  7) В разных плоскостях могут располагаться и параллельные прямые. А также и пересекающиеся прямые Свойства скрещивающихся.  8)Если одна прямая лежит заданной плоскости а вторая прямая пересекает эту плоскость в точке не принадлежащей заданной прямой , то такие прямые являются скрещивающимися

Прямая и плоскость в пространство могут:

а) не иметь общих точек;

б) иметь ровно одну общую точку;

в) иметь хотя бы две общие точки.

В случае а) прямая b параллельна плоскости a: b || a.

В случае б) прямая l пересекает плоскость a в одной точке О;

l   a= О.

В случае в) прямая а принадлежит плоскости a: a   а или а   a.

Теорема. Если прямая b параллельна хотя бы одной прямой а, принадлежащей плоскости a, то прямая параллельна плоскости a.

Предположим, что прямая m пересекает плоскость a в точке. Если m перпендикулярна каждой прямой плоскости a, проходящей через точку Q, то прямая m называется перпендикулярной к плоскости a.

Признаки параллельности прямой и плоскости:

 

1)  Если прямая, лежащая вне плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельна этой плоскости.  

2)  Если прямая и плоскость перпендикулярны одной и той же прямой, то они параллельны.

 

Признаки параллельности плоскостей:

 

1)  Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.

 

2)  Если две плоскости перпендикулярны одной и той же прямой, то они параллельны. 

За угол между прямыми принимают острый угол.

 

  

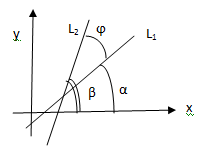
Если прямые параллельны, то k₁=k₂ и  b₁≠b₂

Если прямые перпендикулярны, то k₁*k₂=-1

Если прямые пересекаются, то k₁≠k₂

Если прямые совпадают, то k₁=k₂ и  b₁=b₂ 

 

Угол между двумя прямыми в пространстве

За угол между двумя прямыми в пространстве принимают один из двух смежных углов, который образует прямые, проведенные параллельно данным через какую-нибудь точку в пространстве.

Один из этих углов равен углу между направляющими векторами этих прямых.

 

Где первая прямая задается: 

 

а₁=( m₁, n₁, p₁)

Вторая прямая задается:

 

а₂=( m₂, n₂, p₂)

Если прямые параллельны, то

 

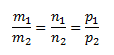
Если прямые перпендикулярны, то m₁ m₂+ n₁ n₂ + p₁ p₂=0.