7.4. Истечение через прямоугольное отверстие и водослив

Рассмотрим истечение через большое (широкое) прямоугольное отверстие (рис. 7.7).

Верхняя кромка отверстия расположена на глубине H₁, а нижняя – на глубине H₂ от свободной поверхности жидкости. Ширина отверстия – b.

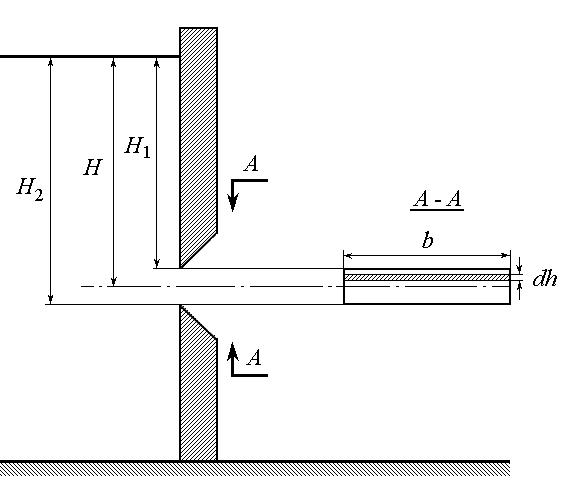
Рис. 7.7

Элементарный расход через прямоугольный элемент площади можно записать как:

.

Для того чтобы найти расход через все отверстие, проинтегрируем выражение для элементарного расхода по h в пределах от H₁ до H₂, считая µ постоянным.

.

Это формула для расхода через прямоугольное отверстие. Но эта формула, как правило, не имеет самостоятельного значения. Она важна как исходная для получения формулы для прямоугольного водослива с тонкой стенкой. Такой водослив получается, если в рассмотренной схеме положим H₁ = 0 (рис. 7.8).

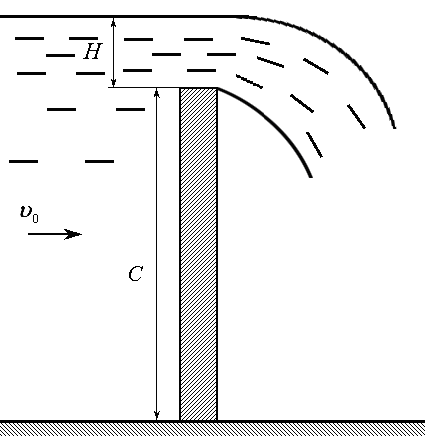
Рис. 7.8

Обозначим . Назовем величину коэффициентом расхода для водослива. Тогда:

.

(7.4)

Значение m в первом приближении можно получить, принимая как для малого круглого отверстия, µ = 0,62. Тогда m ≈ 0,42.

В наших рассуждениях мы не учитывали скорость подхода воды к водосливу и высоту водослива С. С учетом этих величин можно уточнить формулу (7.4).

Условием нормального действия водослива является обеспечение свободного подвода воздуха под струю. Прямоугольный водослив часто используется как измеритель расхода; с этой же целью используются водосливы и иной формы, например, треугольные.

7.5. Истечение при переменном напоре

Рассмотрим опорожнение открытого в атмосферу сосуда произвольной формы через донное отверстие или насадок с коэффициентом расхода µ (рис. 7.9).

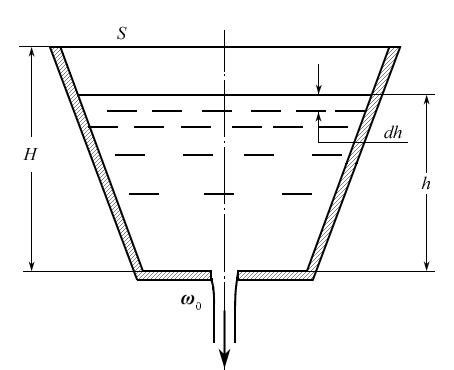
Рис. 7.9

В этом случае истечение будет проходить при переменном, постепенно уменьшающемся напоре. Если напор, а следовательно, и скорость истечения, будут меняться медленно, то движение в каждый момент времени можно рассматривать как установившееся (квазистационарное) и применять для решения уравнение Бернулли.

Обозначим переменную площадь свободной поверхности жидкости S, переменную высоту уровня жидкости, отсчитываемую от дна, – h, площадь отверстия в дне – ω₀. Тогда для бесконечно малого промежутка времени dt справедливо уравнение сохранения объемов

или .

Знак «минус» в формуле возникает потому, что положительному приращению dt соответствует отрицательное приращение dh.

Время полного опорожнения сосуда высотой H найдем, интегрируя это уравнение по переменной высоте уровня в пределах высоты всего сосуда (считаем µ = const):

.

Этот интеграл можно сосчитать, если известен закон изменения площади свободной поверхности S по высоте резервуара. В частности, для призматического сосуда S = const и получаем

.

(7.5)

Числитель этой формулы равен удвоенному объему сосуда, а знаменатель представляет собой расход в начальный момент времени при опорожнении, т. е. при напоре, равном H. Следовательно, время опорожнения сосуда в два раза больше времени истечения такого же объема жидкости при постоянном напоре H.