2. Динамика точки

2.1. Дифференциальные уравнения движения материальной точки

Пусть r - радиус вектор (рис. 1.2) определяющий положение точки в инерциальной системе отсчета.

Рис.1.2.

Тогда ускорение точки

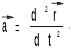
С учетом этого, основное уравнение динамики можно записать в виде:

Полученное выражение является также дифференциальным уравнением движения материальной точки в векторной форме.

Проектируя обе части последнего векторного равенства на оси прямоугольной системы координат получим скалярные выражения представляющие собой дифференциальные уравнения движения точки в осях x, y, z :

Дифференциальные уравнения движения точки при естественном способе задания движения получаются в результате проектирования основного уравнения динамики на оси естественного тетраэдра (рис. 1.3) :

Рис.1.3.

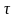- касательная к траектории, n – нормаль, b – бинормаль,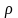 - радиус кривизны траектории.

3. Две основные задачи динамики

3.1. Первая задача. Зная массу точки и закон её движения определяют действующие на точку силы.

Так, если движение точки задано в прямоугольной системе координат, то суть задачи состоит в следующем:

Дано: m , x = f (t) , y = f (t) , z = f (t) .

----------------------------------------------------------

Определить: Fx , Fy , Fz .

В основе решения первой задачи динамики точки лежит дифференцирование её уравнений движения.

3.2.Вторая основная задача динамики

Вторая задача. Зная массу точки и действующие на неё силы определяют закон её движения.

При задании движения точки в прямоугольной системе координат задача имеет вид:

Дано: m , Fx , Fy , Fz .

----------------------------------------------------

Определить: x = f (t) , y = f (t) , z = f (t) .

В основе решения второй задачи динамики лежит интегрирование дифференциальных уравнений движения.. При этом, следует иметь в виду, что сила действующая на материальную точку может быть постоянной или зависить от времени, координат движущейся точки и её скорости. Следовательно, в общем случае, вторая задача динамики сводится к необходимости решения системы дифференциальных уравнений, как например:

m x = Fx ( x, y, z, x, y, z, t )

m y = Fy ( x, y, z, x, y, z, t )

m z = Fz ( x, y, z, x, y, z, t )

в которые искомые функции x, y и z входят вместе со своими первыми и вторыми производными.При решении второй задачи динамики в общем виде решение может быть представлено в виде:

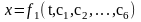
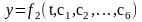
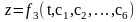
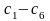- постоянные интегрирования, которые определяются путем подстановки в уравнения начальных условий.

Для определения каждого коэффициента c необходимо в правую часть уравнения вместо времени подставить 0 (t₀ = 0), а в левую часть уравнения начальные значения рассчитываемого параметра.

Таким образом, окончательное решение второй задачи динамики можно представить в виде:

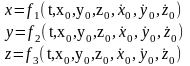
В торая основная задача динамики на практике встречается гораздо чаще. Она подразделяется в зависимости от действующих сил:

1. Сила – постоянная величина

2. Сила зависит от расстояния

3. Сила зависит от скорости

4. Сила зависит от времени