
- •1.Динамика
- •1. Основные определения динамики.
- •2.Основные законы динамики.
- •2. Динамика точки
- •3. Две основные задачи динамики
- •3.2.Вторая основная задача динамики
- •3.Колебания материальной точки
- •2. Свободные колебания материальной точки на пружине
- •Понятие эквивалентной жесткости.
- •3. Свободные колебания математического маятника
- •4. Колебания материальной точки при наличии вязкого трения
- •5. Вынужденные колебания
- •5.Динамика относительного движения материальной точки
- •6.Динамика механической системы
- •7.Моменты инерции твердого тела
- •8.Теорема о моментах инерции относительно параллельных осей (теорема Штейнера)
- •9.Теорема о движении центра масс механической системы
- •10.Общие теоремы динамики точки, механической системы и твердого тела
- •4.1. Теорема об изменении количества движения
- •4.1.1. Количество движения. Импульс силы
- •4.1.2. Теорема об изменении количества движения
- •4.1.3. Следствия из теоремы
- •11.Уравнение Мещерского(основное уравнение динамики тела переменной массы)
- •12.Теорема об изменении кинетического момента механической системы.
- •13.Теорема о зависимости кинетических моментов в относительном движении.
- •14.Теорема об изменении кинетического момента механической системы. Следствие из теоремы
- •15. Теорема об изменении кинетического момента механической системы в её относительном движении по отношению к центру масс
- •16. Дифференциальные уравнения поступательного движения. Дифференциальные уравнения во вращательном движении. Дифференциальные уравнения плоского (плоскопараллельного) движения твердого тела.
- •17. Работа силы. Примеры вычисления работы. Мощность. Кинетическая энергия
- •Кинетическая энергия системы равна сумме кинетических энергий составляющих ее точек. .
- •18. Кинетическая энергия твердого тела в различных случаях его движения. Теорема об изменении кинетической энергии материальной точки. Теорема об изменении кинетической энергии механической системы
- •Кинетическая энергия системы равна сумме кинетических энергий составляющих ее точек. .
- •19. Силовое поле и силовая функция. Критерии потенциальности силового поля. Потенциальная энергия. Потенциальная энергия силы упругости. Закон сохранения полной механической энергии материальной точки
- •20. Принцип Даламбера для материальной точки. Принцип Даламбера для механической системы. Приведение сил инерции к простейшему виду
- •21.Определение реакций опор вращающегося тела
- •22. Основы аналитической механики.
- •Уравнения возможных мощностей и работ
- •23.Понятие об обобщенных координатах и степенях подвижности механических систем. Понятие обобщенной силы.
- •24.Уравнений лагранжа 2-го рода
- •25. Уравнения возможных работ и мощностей в обобщённых силах
- •26. Уравнения лагранжа 2-го рода для консервативных систем
- •27. Элементарная теория удара
- •1. Понятия удара, ударной силы и ударного импульса. Основное уравнение теории удара
- •2. Коэффициент восстановления. Абсолютно упругий и абсолютно неупругий удары. Экспериментальное определение коэффициента восстановления
27. Элементарная теория удара
1. Понятия удара, ударной силы и ударного импульса. Основное уравнение теории удара
Во многих случаях можно наблюдать явление, называемое ударом, когда за достаточно малый промежуток времени скорости точек взаимодействующих тел изменяются на конечную величину.
Если
импульс силы
,
действующей на точку в течение промежутка
времени представить в виде
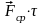 ,
где
,
где
 – среднее значение этой силы за указанное
время, то теорема об изменении количества
движения точки может быть представлена
следующим образом:
– среднее значение этой силы за указанное
время, то теорема об изменении количества
движения точки может быть представлена
следующим образом:
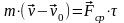 ,
,
где
– скорость точки в конце промежутка
времени
,
а
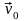 – в начале.
– в начале.
Отсюда
видно, что когда время
стремится к нулю, приращение
 скорости точки также будет величиной
бесконечно малой.
скорости точки также будет величиной
бесконечно малой.
Однако
если модуль силы
будет очень большой (порядка
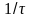 ),
то приращение скорости точки за малый
промежуток времени
окажется величиной конечной, т.е.
произойдет удар.
),
то приращение скорости точки за малый
промежуток времени
окажется величиной конечной, т.е.
произойдет удар.
Силы, при действии которых происходит удар, называются ударными. Ударная сила очень велика и за время удара изменяется в значительных пределах. Найти ее значение во многих случаях не представляется возможным, поэтому в теории удара в качестве меры ударного взаимодействия тел используют понятие ударного импульса:
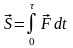 .
.
Ударный импульс, в отличие от ударной силы, является величиной конечной. Неударные силы, которые действуют одновременно с ударными силами, обычно при расчетах не учитываются. Это связано с тем, что неударные силы пренебрежительно малы по сравнению с ударными.
В дальнейшем скорость точки в начале удара будет обозначаться , а в конце удара – . Тогда теорема об изменении количества движения точки при ударе примет вид
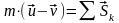 .
.
Изменение количества движения материальной точки за время удара равно сумме действующих на точку ударных импульсов.
Это уравнение называется основным уравнением теории удара и играет в этой теории такую же роль, какую играет основной закон динамики при изучении движения под действием неударных сил.
При рассмотрении механической системы основное уравнение теории удара применяется в следующей форме:
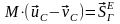 ,
,
где
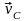 и
и
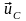 – скорости центра масс системы в начале
удара и в конце удара соответственно;
– масса системы;
– скорости центра масс системы в начале
удара и в конце удара соответственно;
– масса системы;
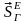 – главный вектор ударных импульсов.
– главный вектор ударных импульсов.
Итак, из полученных результатов вытекает следующее:
1) действием неударных сил (таких, например, как сила тяжести) за время удара можно пренебречь,
2) перемещениями точек тела за время удара можно пренебречь и считать тело во время удара неподвижным,
3) изменения скоростей точек тела за время удара определяются основным уравнением теории удара.
2. Коэффициент восстановления. Абсолютно упругий и абсолютно неупругий удары. Экспериментальное определение коэффициента восстановления
Значение
ударного импульса
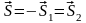 ,
появляющегося при соударении двух тел
(с центрами масс
,
появляющегося при соударении двух тел
(с центрами масс
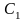 и
и
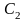 ),
зависит не только от их масс (
),
зависит не только от их масс (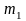 и
и
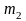 )
и скоростей (
)
и скоростей (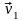 и
и
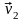 )
вначале удара, но и от упругих свойств
этих тел, которые характеризуют величиной,
называемой коэффициентом
)
вначале удара, но и от упругих свойств
этих тел, которые характеризуют величиной,
называемой коэффициентом
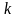 восстановления.
восстановления.

В
большинстве случаев допускают, что
взаимодействующие тела являются
гладкими. При этом ударные импульсы
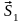 и
и
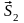 направлены по общей нормали к контактирующим
поверхностям.
направлены по общей нормали к контактирующим
поверхностям.
Коэффициент восстановления – физическая величина, равная отношению модуля нормальной составляющей относительной скорости точки контакта тел после удара к его значению до удара.
Рассмотрим
процесс удара, который обычно разбивается
на две фазы. В течение первой фазы
проекция на нормаль
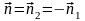 относительной
скорости точки контакта тел,
т.е.
относительной
скорости точки контакта тел,
т.е.
 ,
постепенно уменьшается по величине до
нуля. При этом тела деформируются. Во
второй фазе тела постепенно частично
восстанавливают свои формы и размеры,
а относительная скорость точки контакта
при этом увеличивается по величине, но
не достигает того значения, которое
имела в самом начале первой фазы удара.
Из всего этого можно сделать два важных
вывода.
,
постепенно уменьшается по величине до
нуля. При этом тела деформируются. Во
второй фазе тела постепенно частично
восстанавливают свои формы и размеры,
а относительная скорость точки контакта
при этом увеличивается по величине, но
не достигает того значения, которое
имела в самом начале первой фазы удара.
Из всего этого можно сделать два важных
вывода.
Первый – для осуществления удара в начале первой фазы должно выполняться условие
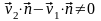 .
.
И второй – относительная скорость точки контакта тел в течение первой фазы удара противоположна по знаку относительной скорости точки контакта в течение второй фазы этого удара.
Итак,
пусть
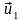 и
и
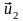 – скорости контактных точек тел после
удара, а
и
– скорости этих же точек, но до удара.
Тогда
– скорости контактных точек тел после
удара, а
и
– скорости этих же точек, но до удара.
Тогда
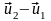 и
и
 – относительные скорости точки контакта
после удара и до удара соответственно.
Проекции этих скоростей на нормаль
– относительные скорости точки контакта
после удара и до удара соответственно.
Проекции этих скоростей на нормаль
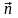 :
:
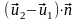 и
и
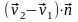 .
.
В соответствии с определением, коэффициент восстановления, т.е.
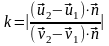 .
.
Учитывая, что относительная скорость при ударе меняет направление, получим окончательно, что
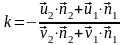 .
.
Если
 ,
то удар является абсолютно
упругим,
а если
,
то удар является абсолютно
упругим,
а если
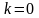 – то удар абсолютно
неупругий.
Явлений абсолютно упругого и абсолютно
неупругого ударов на практике не бывает.
Эти понятия используются в ряде случаев
для упрощения расчетов. При этом при
абсолютно упругом ударе тела полностью
восстанавливают свои формы и размеры
во второй фазе удара, а при абсолютно
неупругом ударе форма и размеры тел в
течение удара изменяются и не
восстанавливаются.
– то удар абсолютно
неупругий.
Явлений абсолютно упругого и абсолютно
неупругого ударов на практике не бывает.
Эти понятия используются в ряде случаев
для упрощения расчетов. При этом при
абсолютно упругом ударе тела полностью
восстанавливают свои формы и размеры
во второй фазе удара, а при абсолютно
неупругом ударе форма и размеры тел в
течение удара изменяются и не
восстанавливаются.
Коэффициент восстановления измеряют следующим образом.

Рассмотрим
шар, падающий вертикально на неподвижную
горизонтальную жесткую плиту. В течение
первой фазы скорости частиц шара, равные
в момент начала удара
(движение шара считаем поступательным),
убывают до нуля; при этом скорость плиты,
т.е.
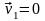 .
Шар деформируется и вся его начальная
кинетическая энергия переходит во
внутреннюю потенциальную энергию
деформации. Во второй фазе удара шар
под действием внутренних сил (т.е. сил
упругости) начинает восстанавливать
свою форму; при этом его внутренняя
потенциальная энергия переходит в
кинетическую энергию движения частиц
шара. В конце удара скорости частиц
будут равны
.
Однако полностью механическая энергия
шара при этом не восстанавливается, так
как часть ее уходит на сообщение шару
остаточных деформаций и его нагревание.
Поэтому скорость
будет меньше скорости
.
Скорость плиты после удара, т.е.
.
Шар деформируется и вся его начальная
кинетическая энергия переходит во
внутреннюю потенциальную энергию
деформации. Во второй фазе удара шар
под действием внутренних сил (т.е. сил
упругости) начинает восстанавливать
свою форму; при этом его внутренняя
потенциальная энергия переходит в
кинетическую энергию движения частиц
шара. В конце удара скорости частиц
будут равны
.
Однако полностью механическая энергия
шара при этом не восстанавливается, так
как часть ее уходит на сообщение шару
остаточных деформаций и его нагревание.
Поэтому скорость
будет меньше скорости
.
Скорость плиты после удара, т.е.
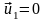 .
.
При этом:
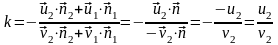 .
.
Действительный коэффициент восстановления всегда меньше 1.
Для
расчета коэффициента
измеряют
высоты
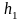 и
и
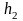 – откуда шар начал падать и куда шар
отскочил соответственно. По формуле
Галилея скорость
– откуда шар начал падать и куда шар
отскочил соответственно. По формуле
Галилея скорость
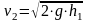 ,
а скорость
,
а скорость
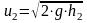 .
.
Поэтому
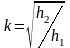 .
.
Значение
коэффициента восстановления для тел
из различных материалов дается в
соответствующих справочниках. В
частности, можно считать, что при
скоростях соударения порядка 3 м/с при
ударе дерева о дерево
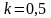 ,
стали о сталь
,
стали о сталь
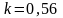 ,
стекла о стекло
,
стекла о стекло
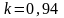 .
.
