Уравнения возможных мощностей и работ

Располагаясь в инерциальной системе отсчёта к рассмотрению принимаем произвольную механическую систему, в любой возможной её

конфигурации.Поясняем понятие «конфигурация»: игла швейной машины может быть в верхнем положении, чему будет соответствовать определённая совокупность положений других деталей, приводящих её в движение; при среднем положении иглы конфигурация деталей в швейной машине будет другой; в нижнем - третьей и т.д. Пусть принятая к рассмотрению механическая система находится под действием любого действительного комплекса сил. Принятую к рассмотрению механическую систему представляем состоящей из частиц. Для каждой из них на основании рассмотренного в предыдущем разделе записываем:

*

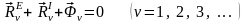Вышеприведенная запись - это множество записанных в столбец равенств – второе под первым, третье под вторым и т.д. (с индексами ).

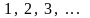Принимаем также к рассмотрению любое возможное перемещение этой системы (при решении конкретной задачи – простейшее). Возможную скорость 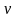-той частицы обозначаем .

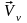
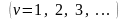Умножаем равенства скалярно на возможные скорости. Получаем:

.

Почленно складываем столбец равенств (б):

.

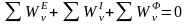Итак, получено уравнение возможных мощностей: -

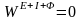Для любой механической системы, при любой возможной её конфигурации и на любом возможном перемещении суммарная возможная мощность действующих на неё внешних, внутренних и даламберовых сил инерции равна нулю.Предадим системе возможное перемещение. Каждая ее точка переместится на некоторую виртуальную величину 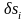. Умножаем равенства * скалярно на . Получим уравнение возможных работ: -

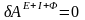Для любой механической системы, при любой возможной её конфигурации и на любом возможном перемещении суммарная возможная работа действующих на неё внешних, внутренних и даламберовых сил инерции равна нулю.Если механическая система состоит из абсолютно твёрдых тел и нерастяжимых нитей, а трением в трущихся друг о друга телах пренебрегается (по причине их малости во многих конкретно решаемых задачах), то внутренние силы можно не учитывать, а системы, в которых суммарные мощности (и работы) внутренних сил равны нулям, называют механическими системами с идеальными связями.

Для механических систем с идеальными связями выше полученные математические выражения принимают вид: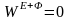 -общее уравнение динамики в форме через возможные мощности;

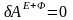- общее уравнение динамики в форме через возможные работы

Для механических систем с идеальными связями, при любых возможных их конфигурациях и на любых возможных перемещениях суммарная возможная мощность (работа) действующих внешних сил и даламберовых сил инерции равна нулю.

Для механических систем, в которых отсутствует перемещение тел, действующие на частицы силы инерции равны нулю. Равны нулю мощности и работы всех внутренних сил. Мысленно выделяемые из таких механических систем подсистемы возможными движениями обладают. Применяемые к ним уравнения принимают вид:

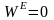- общее уравнение статики в форме через возможные мощности.

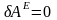- общее уравнение статики в форме через возможные работы:

Если ранее изученную совокупность методов решения задач статики называют «геометрической статикой», то изучаемые здесь методы решения задач статики называют «Кинематической (или Аналитической) статикой».

Методика решения задач с помощью принципа возможных перемещений (одна степень свободы):

1. Задаем системе возможные перемещения. Для этого сообщаем одному звену возможное перемещение и изображаем на схеме как переместятся остальные звенья с учетом наложенных связей.

2. Составляем уравнения элементарных работ (мощностей) внешних активных сил.

3. Выразим все перемещения (скорости) через какое-то одно, сокращаем его и решаем уравнение.

Данный принцип удобно использовать для нахождения реакций связи. При этом искомую реакцию связи представляем в виде внешней активной силы, способной сообщить возможное перемещение системе.