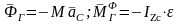- •1.Динамика
- •1. Основные определения динамики.
- •2.Основные законы динамики.
- •2. Динамика точки
- •3. Две основные задачи динамики
- •3.2.Вторая основная задача динамики
- •3.Колебания материальной точки
- •2. Свободные колебания материальной точки на пружине
- •Понятие эквивалентной жесткости.
- •3. Свободные колебания математического маятника
- •4. Колебания материальной точки при наличии вязкого трения
- •5. Вынужденные колебания
- •5.Динамика относительного движения материальной точки
- •6.Динамика механической системы
- •7.Моменты инерции твердого тела
- •8.Теорема о моментах инерции относительно параллельных осей (теорема Штейнера)
- •9.Теорема о движении центра масс механической системы
- •10.Общие теоремы динамики точки, механической системы и твердого тела
- •4.1. Теорема об изменении количества движения
- •4.1.1. Количество движения. Импульс силы
- •4.1.2. Теорема об изменении количества движения
- •4.1.3. Следствия из теоремы
- •11.Уравнение Мещерского(основное уравнение динамики тела переменной массы)
- •12.Теорема об изменении кинетического момента механической системы.
- •13.Теорема о зависимости кинетических моментов в относительном движении.
- •14.Теорема об изменении кинетического момента механической системы. Следствие из теоремы
- •15. Теорема об изменении кинетического момента механической системы в её относительном движении по отношению к центру масс
- •16. Дифференциальные уравнения поступательного движения. Дифференциальные уравнения во вращательном движении. Дифференциальные уравнения плоского (плоскопараллельного) движения твердого тела.
- •17. Работа силы. Примеры вычисления работы. Мощность. Кинетическая энергия
- •Кинетическая энергия системы равна сумме кинетических энергий составляющих ее точек. .
- •18. Кинетическая энергия твердого тела в различных случаях его движения. Теорема об изменении кинетической энергии материальной точки. Теорема об изменении кинетической энергии механической системы
- •Кинетическая энергия системы равна сумме кинетических энергий составляющих ее точек. .
- •19. Силовое поле и силовая функция. Критерии потенциальности силового поля. Потенциальная энергия. Потенциальная энергия силы упругости. Закон сохранения полной механической энергии материальной точки
- •20. Принцип Даламбера для материальной точки. Принцип Даламбера для механической системы. Приведение сил инерции к простейшему виду
- •21.Определение реакций опор вращающегося тела
- •22. Основы аналитической механики.
- •Уравнения возможных мощностей и работ
- •23.Понятие об обобщенных координатах и степенях подвижности механических систем. Понятие обобщенной силы.
- •24.Уравнений лагранжа 2-го рода
- •25. Уравнения возможных работ и мощностей в обобщённых силах
- •26. Уравнения лагранжа 2-го рода для консервативных систем
- •27. Элементарная теория удара
- •1. Понятия удара, ударной силы и ударного импульса. Основное уравнение теории удара
- •2. Коэффициент восстановления. Абсолютно упругий и абсолютно неупругий удары. Экспериментальное определение коэффициента восстановления
20. Принцип Даламбера для материальной точки. Принцип Даламбера для механической системы. Приведение сил инерции к простейшему виду
Применение метода кинетостатики в теоретической механике даёт возможность решать методами статики многие задачи динамики. Особенно удобно использовать этот метод для учёта динамических нагрузок при силовых расчётах инженерных сооружений и конструкций.
Метод кинетостатики требует введение нового термина Даламберовых сил инерции.
Термин
«сила инерции» уже встречался при
изучении сложного движения точки. Но
там речь шла о переносной (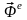 )
и кориолисовой (
)
и кориолисовой (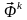 )
силах инерции, которые принято называть
эйлеровыми силами инерции. Даламберова
сила инерции (
)
силах инерции, которые принято называть
эйлеровыми силами инерции. Даламберова
сила инерции (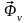 )
- это другое понятие; это понятие,
связанное с ускорением частицы
относительно инерциальной системы
отсчёта. Если даламберову силу инерции
связать с ускорениями относительно
неинерциальной системы, то она окажется
суммой трёх составляющих – двух эйлеровых
и относительной (
)
- это другое понятие; это понятие,
связанное с ускорением частицы
относительно инерциальной системы
отсчёта. Если даламберову силу инерции
связать с ускорениями относительно
неинерциальной системы, то она окажется
суммой трёх составляющих – двух эйлеровых
и относительной (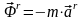 )
сил инерции, т.е.:
)
сил инерции, т.е.:
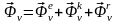 .
.
Среди учёных до сих пор возникают споры о физическом смысле сил инерции
Существует 3 версии возникновения этой силы:
Сила инерции не существует в природе – это искусственно вводимая математическая величина, применяемая для принципа Даламбера
2. Сила инерции – физическая сила реально существующая, но прикладывается она не к материальной точке, а к телам, сообщающим ускорения этой точке.
3. Силы инерции реально существуют в собственной системе отсчета материальной точки.
Сила инерции – это вектор, имеющий размерность силы, по модулю равный произведению массы на ускорение, направленный противоположно ему, который можно включать в систему действующих на частицу сил и в процессе математических преобразований обращаться с ним, как с обычной силой.
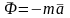
В зависимости от ускорения точки силы инерции бывают касательные и нормальные.
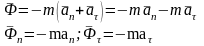
При вращательном движении силы инерции подразделяются на центростремительные и вращательные
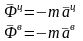
Принцип Даламбера для материальной точки
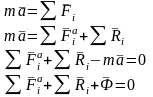
где
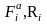 -
активные
силы и реакции связей соответственно.
-
активные
силы и реакции связей соответственно.
Таким образом, принцип Даламбера для материальной точки имеет следующую трактовку.
Система активных сил, действующих на точку, реакций связей и силы инерции является равновесной.
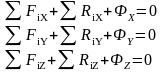
Проекции на оси естественного трехгранника
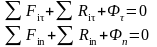
П римеры:
римеры:
1. Лифт массой 300 кг поднимается ускоренно (а = 4 м/с2). Определить натяжение троса.
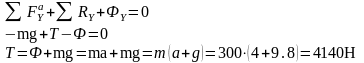
2. Конический маятник с длиной нити l, массой груза m, вращается вокруг оси с угловой скоростью ω. Определить зависимость угла наклона нити (α) от вертикали от постоянной угловой скорости.
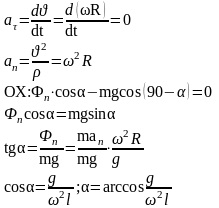

3 .
Автомобиль массой 2 т движется по мосту
R
= 50 м со скоростью 20 м/с. Определить
давление автомобиля на мост в его
середине.
.
Автомобиль массой 2 т движется по мосту
R
= 50 м со скоростью 20 м/с. Определить
давление автомобиля на мост в его
середине.
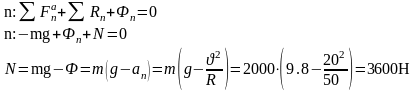
Принцип Даламбера для механической системы
На каждую точку системы действуют как внешние, так и внутренние силы. Поэтому принцип Даламбера для точки системы Запишется:
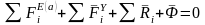
Просуммируем для всех точек системы:
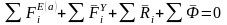
Т. к. сумма внутренних сил равна нулю, получим:
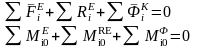 (1)
(1)
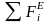 -
сумма внешних активных сил
-
сумма внешних активных сил
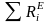 -
сумма реакций связи со стороны тел, не
входящих в систему
-
сумма реакций связи со стороны тел, не
входящих в систему
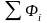 -
сумма сил инерции точек
-
сумма сил инерции точек
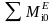 -
сумма моментов внешних активных сил
относительно некоторого произвольного
центра О
-
сумма моментов внешних активных сил
относительно некоторого произвольного
центра О
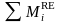 -
сумма моментов внешних реакций
относительно того же центра
-
сумма моментов внешних реакций
относительно того же центра
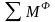 -
сумма моментов сил инерции относительно
того же
центра
-
сумма моментов сил инерции относительно
того же
центра
Проектируем уравнения (1) на координатные оси

Уравнения (1) можно представить в следующем виде:
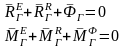
Таким образом, условия динамического равновесия имеют вид-
 -
-
Главные вектор и момент от внешних и даламберовых сил инерции равны нулю для любой механической системы.
Приведение сил инерции к простейшему виду
Для
всех случаев движения главный вектор
всех сил инерции системы равен:
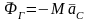
Приведение сил инерции к простейшему виду в различных случаях движения системы
№ |
Вид движения |
К чему приводятся силы инерции |
1 |
Поступательное |
|
2 |
Вращение вокруг оси перпендикулярной плоскости материальной симметрии |
или
отстоящей
от оси z
на расстоянии
|
3 |
Вращение вокруг оси, проходящей через центр масс |
|
4 |
Плоскопараллельное движение |
|
В подавляющем большинстве случаев главный вектор сил инерции прикладывается в центре масс системы.
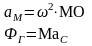


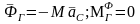
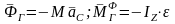
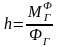 .
.