1.Динамика
Динамика – раздел теоретической механики, в котором изучается движение тел под действием сил.
Динамика - наиболее общий раздел механики. Так, среди практических задач механики лишь их небольшое число требует чисто статического или кинематического исследования. В большинстве случаев, проводиться полное, динамическое изучение тех или иных явлений. В этом плане статику и кинематику можно рассматривать как введение в динамику, хотя они имеют и самостоятельное прикладное значение.
В основу динамики положены исходные положения (аксиомы) впервые высказанные Ньютоном и Галилеем в 17 веке.
1. Основные определения динамики.
Основные законы динамики сформулированы применительно к материальной точке.
В основе классической механики лежат два допущения. Последними утверждается существвование абсолютного пространства и абсолютного времени. Полагается, что пространство обладает чисто геометрическими свойствами, а время не зависит от движения системы отсчета.
В динамике принимается также, что массы движущихся материальных объектов не зависят от скорости их движения.
Масса – мера инертных и гравитационных свойств тела. Измеряется в системе СИ в килограммах. [m] = [кг].
Это такая система отсчета, которой справедлив закон инерции.
2.Основные законы динамики.
2.1. Закон инерции: (первый закон Ньютона) если действующая на материальную точку система сил уравновешена или эквивалентна нулю, то точка находится либо в покое, либо в состоянии прямолинейного движения.
Изолированная материальная точка находится в состоянии покоя или равномерного и прямолинейного движения.
Под изолированной, понимается материальная точка не взаимодействующая с другими телами или когда силы действующие на точку, взаимно уравновешиваются.
Система отсчета в которой выполняется первый закон Ньютона, т.е. система в которой изолированная материальная точка движется равномерно и прямолинейно или находится в состоянии покоя называется инерциальной системой отсчета. Инерциальная система отсчета – система отсчета, которую можно считать неподвижной.
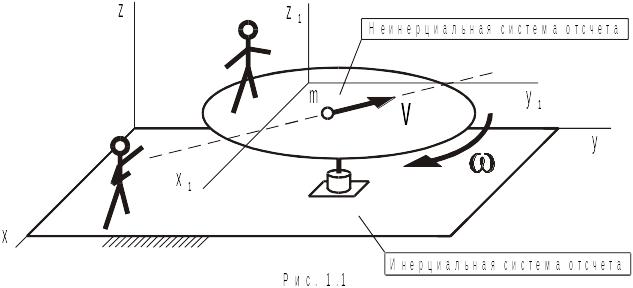
Система отсчета не обладающая этими свойствами, называются неинерциальной системой отсчета. В последней, точка на которую не действуют силы, движется с ускорением и её скорость может меняться как по величине, так и по направлению (рис. 1.1). Неинерциальная система отсчета – движущаяся система отсчета. При решении задач чаще всего за инерциальную систему отсчета принимают геоцентрическую (связанную с землей) систему отсчета. При расчете объектов больших масс и с большими скоростями за инерциальную систему отсчета можно принять гелиоцентрическую (связанную с солнцем) систему отсчета.
2.2. Основной закон динамики: этим законом является второй закон Ньютона.
В аналитической форме этот закон представляет основное уравнение динамики
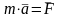
где F - сила, a - ускорение, m - масса, являющаяся мерой инертных свойств материальной точки.
Ускорение тела пропорционально силе вызывающей это ускорение.
Или: сила действующая на материальную точку, сообщает ей ускорение, которое в инерциальной системе отсчета пропорционально величине и имеет направление силы.
Единица массы в системе СИ - 1 кг. Один килограмм равен массе 1 дм3 чистой воды при температуре 40 С. Единица силы - 1 Ньютон (1Н). Один Ньютон - сила сообщающая массе 1 кг ускорение 1 м/с2.
2.3. Третий закон Ньютона (Закон равенства действия и противодействия)
Две материальные точки взаимодействуют друг с другом с силами равными по величине и направленными в противоположные стороны.
2.4. Закон независимости действия сил. (Закон суперпозиции).
При действии на материальную точку нескольких сил её ускорение равно сумме ускорений, которые имела бы точка при действии на неё каждой силы в отдельности.
Это значит, что при действии на материальную точку сил F1, F2, …, Fn, каждая из которых сообщает точке ускорения а1, а2, … аn, ускорение
a = a1 + a2 + … + an .
На основании второго закона Ньютона
m a1 = F1 , m a2 = F2 , … , m an = Fn .
Складывая эти равенства, получим
m ( a1 + a2 + … + an ) = F1 + F2 + … + Fn ,
или, на основании закона независимости сил
m
a = F1
+
F2
+
… + Fn
=
,
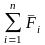где Fi - равнодействующая всех сил, приложенных к материальной точке.
Таким образом, движение материальной точки под действием сил F1, F2, … , Fn , будет таким же, как и при действии одной силы, равной их геометрической сумме (равнодействующей).
Выражение
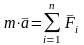называют основным уравнением динамики
материальной точки.