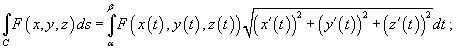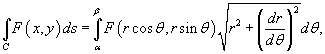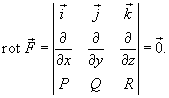- •23.5. Приложения двойных интегралов 23.5.1. Геометрические приложения
- •Достаточное условие существования тройного интеграла
- •Механическая трактовка тройного интеграла
- •Вычисление тройного интеграла в декартовых координатах
- •Интегрирование полных дифференциалов
- •Решение дифференциальных уравнений с помощью рядов
Понятие двойного интеграла теорема сущ-ния
Свойства двойного интеграла
Двойной интеграл обладает следующими свойствами:
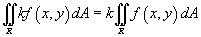 ,
где k -
константа;
,
где k -
константа;
Если
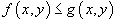 в
области R,
то
в
области R,
то 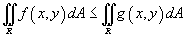 ;
;
Если
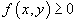 в
области R и
в
области R и 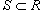 (рисунок
4), то
(рисунок
4), то 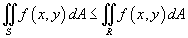 ;
;
Если на R и области R и S являются непересекающимися (рисунок 5), то
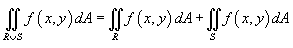 .
Здесь
.
Здесь  означает
объединение этих двух областей.
означает
объединение этих двух областей.
Определение двойного интеграла
Понятие интеграла может быть расширено на функции двух и большего числа переменных. Рассмотрим, например, функцию двух переменных z = f (x,y). Двойной интеграл от функции f (x,y) обозначается как
![]()
где R -
область интегрирования в плоскости
Oxy.
Если определенный интеграл ![]() от
функции одной переменной
от
функции одной переменной ![]() выражает
площадь под кривой f (x) в
интервале от x
= a до x
= b, то двойной
интеграл выражает объем под поверхностью z
= f (x,y) выше
плоскости Oxy в
области интегрирования R
выражает
площадь под кривой f (x) в
интервале от x
= a до x
= b, то двойной
интеграл выражает объем под поверхностью z
= f (x,y) выше
плоскости Oxy в
области интегрирования R
Двойные интегралы в полярных координатах |
|
Одним из частных случаев замены переменных является переход из декартовой в полярную систему координат (оооооооооо)
|
кобиан такого преобразования имеет вид
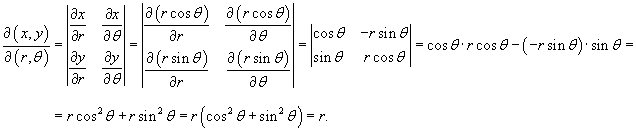
Следовательно, дифференциальный элемент в полярных координатах будет равен
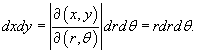
Пусть область интегрирования R в полярных координатах определяется следующим образом (рисунок 2):
![]()
Тогда двойной интеграл в полярных координатах описывается формулой
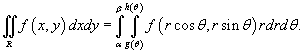
Вычисление двойного интеграла в декартовой системе координат для правильной области
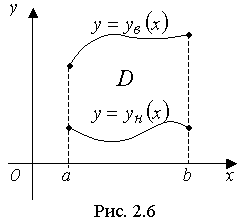
Пусть область D - правильная в отношении оси Ох (рис. 2.6.)
Тогда в этом случае область D может быть задана одной системой неравенств:
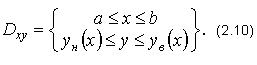
Если
существует двойной интеграл
 (это
возможно, например, если f(x;
y) непрерывна
на D),
то его можно вычислить через повторный
кратный интеграл так:
(это
возможно, например, если f(x;
y) непрерывна
на D),
то его можно вычислить через повторный
кратный интеграл так:
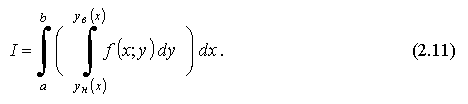 При
этом внутренний интеграл по у находится
при постоянном х.
При
этом внутренний интеграл по у находится
при постоянном х.
Данное представление (2.11) получается из определения двойного интеграла при специальном способе разбиения области D на n "мелких" частей (линиями, параллельными либо Ох, либо Оу - прямоугольной "шахматной" сеткой. А затем выполняется суммирование "объёмов" ΔVi сначала по оси Оу, а затем по оси Ох).
23.5. Приложения двойных интегралов 23.5.1. Геометрические приложения
Вычисление
площадей плоских фигур![]()
Пример:![]()
Определим
точки пересечения кривых: х-2-![]() +
х - 2 = О,
+
х - 2 = О,
![]() =
-2;1;
=
-2;1;![]() (-2,-2),
(-2,-2),![]() (1,
1) (рис. 23.9).
(1,
1) (рис. 23.9).
![]()
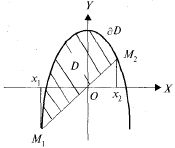
Рис. 23.9
Рис. 23.10
Вычисление объемов цилиндрических тел
![]() (см.
разд. 23.1).
(см.
разд. 23.1).
Пример:![]() (рис.
23.11). V = ?
(рис.
23.11). V = ?
![]()
![]()
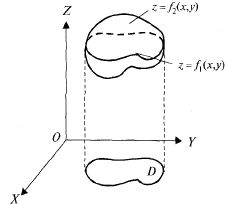
Замечание.
Если тело, объем которого нужно найти,
ограничено сверху поверхностью![]() а
снизу
а
снизу![]() причем
проекцией обеих поверхностей на плоскость
XOY является область D, то объем V этого
тела (рис. 23.11) вычисляется по формуле
причем
проекцией обеих поверхностей на плоскость
XOY является область D, то объем V этого
тела (рис. 23.11) вычисляется по формуле
![]()
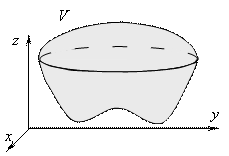
ОПРЕДЕЛЕНИЕ ТРОЙНОГО ИНТЕГРАЛА |
||
Тройным интегралом от функции f(x, y, z) по области V называется конечный предел трехмерной интегральной суммы при стремлении к нулю ранга разбиения, порождающего эту сумму (если этот предел существует и не зависит ни от способа разбиения области V на элементарные части, ни от выбора точек на каждой из этих элементарных частей):
здесь n – это количество элементарных частей разбиения области V; Pi (xi,yi,zi) – произвольно выбранная точка на каждой элементарной части, i = 1,...,n;
|
Достаточное условие существования тройного интеграла
Если
функция f (x,y,z)
непрерывная в замкнутой области V,
то ![]() существует.
существует.
Механическая трактовка тройного интеграла
Если f (x,y,z) 0
— это объемная плотность распределения
вещества в области V,
то ![]() —
это масса всего вещества в трехмерной
области V.
—
это масса всего вещества в трехмерной
области V.
Основные свойства тройного интеграла
Аналогичны
свойствам определенного интеграла по
отрезку ![]() и
двойного интеграла по области D.
и
двойного интеграла по области D.
Свойство 1 (линейность тройного интеграла по подынтегральной функции)
![]() ,
,
где ![]() —
постоянные множители по x, y, z.
—
постоянные множители по x, y, z.
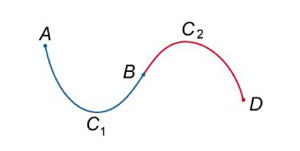
Свойство 2 (аддитивность тройного интеграла по области интегрирования)
Если V = V1 V2,
то ![]() .
.
Свойство 3 (о значении тройного интеграла от функции, тождественно равной единице)
Если
подынтегральная функция f(x,y,z) 1
для ![]() ,
то тройной интеграл от неё по области V равен
объему (мере) области интегрирования:
,
то тройной интеграл от неё по области V равен
объему (мере) области интегрирования:
![]()
(здесь область V и её объём V обозначены одной буквой).
Свойство 4 (оценки значения тройного интеграла)
Если m и M — наименьшее и наибольшее значения функции f(x,y,z) в замкнутой области V, то
![]()
Если
|f(x,y,z)|![]() при (x,y,z)V,
то
при (x,y,z)V,
то
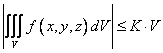
Свойство 5 (теорема о среднем значении подынтегральной функции)
Если функция f (x,y,z) непрерывна в области V, то существует хотя бы одна точка P0(x0;y0;z0)V такая, что
![]()
При
этом число 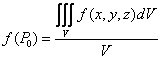 называется средним
значением
называется средним
значением
функции f(x,y,z) по области V.
Вычисление тройного интеграла в декартовых координатах
Вычисление тройного интеграла сводится к вычислению трехкратного интеграла.
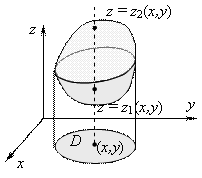

В декартовых координатах область V, правильная в направлении оси OZ, записывается системой неравенств
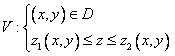 ,
,
где D –
это проекция области V на
плоскость XOY, а поверхности ![]() и
и ![]() ограничивают
область V соответственно
снизу и сверху (Рис.
6).
ограничивают
область V соответственно
снизу и сверху (Рис.
6).
Если
двумерную область D также
записать системой неравенств 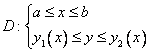 ,
то трехмерная область V запишется
системой трех неравенств
,
то трехмерная область V запишется
системой трех неравенств 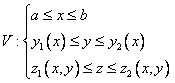
Тогда тройной интеграл сводится сначала к двойному, а затем к трёхкратному с учётом того, что в декартовых координатах dV = dxdydz;
формула сведения тройного интеграла к трехкратному интегралу имеет следующий вид:
|
(1) |
Существует всего 6 вариантов сведения тройного интеграла к трехкратному в декартовых координатах (в зависимости от выбранного порядка интегрирования).
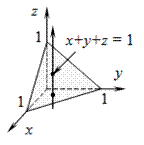
Пример 1 (вычисление тройного интеграла в декартовых координатах)
Вычислить ![]() , где область V ограничена поверхностями
, где область V ограничена поверхностями ![]() .
.
Решение
|
|
Запишем область V системой трёх неравенств: |
Сводим тройной интеграл к трехкратному по формуле (1) в соответствии с системой
неравенств и вычисляем трехкратный интеграл:
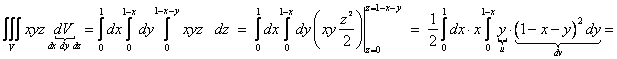

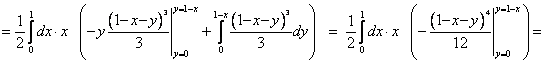
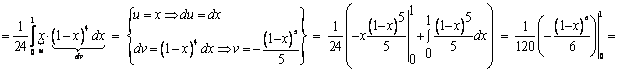
![]() .
.
|
Тройные интегралы в сферических координатах |
||||||
|
||||||
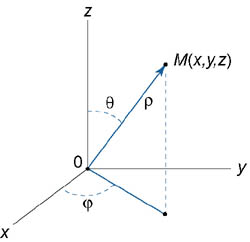
Сферическими координатами точки M(x,y,z) называются три числа − ρ, φ, θ , где
ρ −
длина радиуса-вектора точки M;
φ −
угол, образованный проекцией
радиуса-вектора
Обратите внимание, что определения ρ, φ в сферических и цилиндрических координатах отличаются друг от друга. Сферические координаты точки связаны с ее декартовыми координатами соотношениями
Якобиан перехода от декартовых координат к сферическим имеет вид:
Раскладывая определитель по второму столбцу, получаем
Соответственно, абсолютное значение якобиана равно
Следовательно, формула замены переменных при преобразовании декартовых координат в сферические имеет вид:
Тройной интеграл удобнее вычислять в сферических координатах, когда область интегрирования U представляет собой шар (или некоторую его часть) и/или когда подынтегральное выражение имеет видf (x2 + y2 + z2). Иногда выгодно использовать т.н. обощенные сферические координаты, связанные с декартовыми формулами
В этом случае якобиан равен
|
Криволинейные интегралы первого рода |
||||||
|
||||||
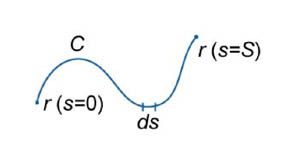
Определение
Пусть
кривая C описывается
векторной функцией
Криволинейный
интеграл
Свойства криволинейного интеграла первого рода Криволинейный интеграл I рода обладает следующими свойствами:
где
кривая C задана
в полярных координатах функцией |
Формула Грина связывает двойной интеграл по плоской области с криволинейным интегралом по контуру этой области.
Пусть
функции P(x,y),
Q(x,y), P'y(х,у),
Q'x(х,у) непрерывны
в замкнутой области D,
ограниченной контуром L (рис.
3.6).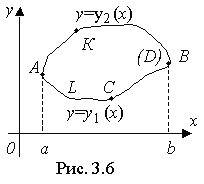
Пусть контур L, кроме того, пересекается прямыми, параллельными осям координат, не более чем в двух точках.
Пусть уравнение АСВ есть y = y1(x) при a ≤ x ≤ b , и уравнение АКВ есть y = y2(x) при a ≤ x ≤ b.
Преобразуем двойной интеграл:
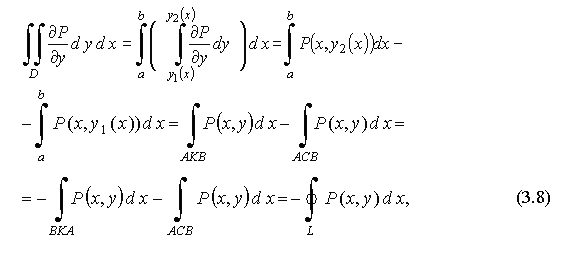
здесь
символ ![]() означает
криволинейный интеграл по замкнутому
контуру L.
означает
криволинейный интеграл по замкнутому
контуру L.
Аналогично получается
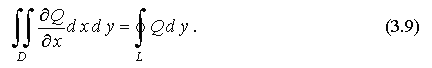
Вычитая из формулы (3.9) формулу (3.8), получаем формулу Грина
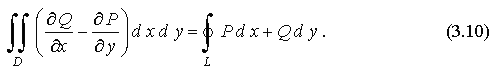
Независимость криволинейных интегралов от пути интегрирования |
|
Определения
Криволинейный
интеграл второго рода от векторной
функции
В
этом случае криволинейный интеграл
второго рода от функции
(Здесь можно увидеть аналогию с формулой Ньютона-Лейбница для определенных интегралов.) Таким образом, если криволинейный интеграл не зависит от пути интегрирования, то для любого замкнутого контура C справедливо соотношение
Векторное
поле, обладающее свойством Признак потенциальности поля Криволинейный интеграл II рода от функции не зависит от пути интегрирования, если
Предполагается, что каждый компонент функции имеет непрерывные частные производные по переменным x, y и z. Если криволинейный интеграл рассматривается в плоскости Oxy, то в случае потенциального поля будет справедливо соотношение
В этом случае признак потенциальности векторного поля упрощается и принимает вид
Рассмотренный признак является необходимым, но, вообще говоря, не достаточным для потенциальности поля. Данное условие достаточно, если только область интегрирования D односвязна. |

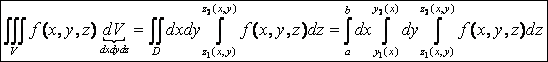
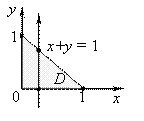

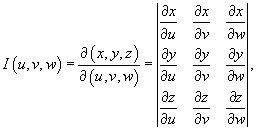
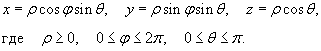
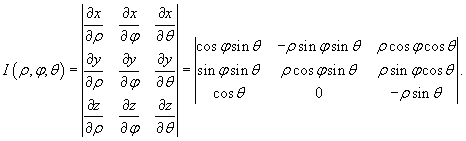
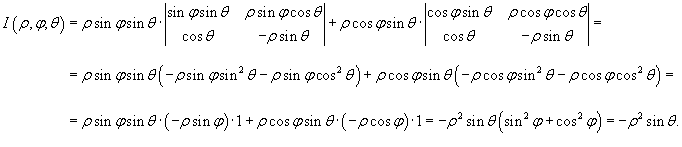
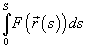 называется криволинейным
интегралом первого рода от
скалярной функции F вдоль
кривой C и
обозначается как
называется криволинейным
интегралом первого рода от
скалярной функции F вдоль
кривой C и
обозначается как