26. Квадратичные формы. Приведение квадратичной формы к каноническому виду.

Квадратичная форма от n переменных – сумма всевозможных попарных произведений этих переменных

Ф(x, y, z) = a₁₁x² + a₁₂xy+ a₁₃xz + a₂₁yx + a₂₂y² + a₂₃yz + a₃₁zx +a₃₂zy +a₃₃z²

Матрица квадратичной формы симметрична относительно главной диагонали

Квадратичная форма называется канонической, если в ней отсутствуют смешанные произведения

Ф(x, y, z) = a₁₁x² + a₂₂y² +a₃₃z²

Любую квадратичную форму можно единственным образом привести к каноническому виду, тогда в ее матрице на главной диагонали будут стоять ее собственные числа

Приведение квадратичной формы к каноническому виду осуществляется по формуле A’ = T^TAT

T – это матрица перехода, составляется из собственных векторов, показывает как меняется система координат (1 строка: x=x₁cosα – y₁sinα + 0z_1, 2 строка:y=x₁sinα + y₁cosα + 0z_1; 3 строка z=...)

27. Системы координат на плоскости. Преобразования системы координат. Деление отрезка в данном отношении. Уравнения линий на плоскости.

- связь

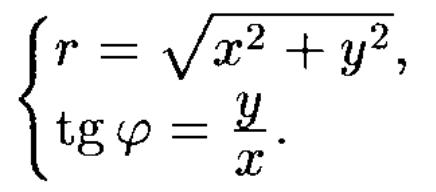- связь ^

Преобразование системы координат:

Параллельный перенос: 0₁ (a; b) – начало координат в новой системе

M (x; y) – точка в старой системе

M (x₁; y₁) – точка в новой системе

Очевидно, что x₁ = x - a; y₁ = y – b. Чтобы узнать величину a и b, нужно выделить полные квадраты в общем уравнении кривой

Поворот: α – угол поворота; φ – угол между радиус-векторами точки M и новой осью координат

x = r_m*cos(φ+α)

y = r_m*sin(φ+α)

x = r (cosφ cosα – sinφ sinα)

y = r (cosφ sin α + sin φ cos α)

x = r cosφ cosα – r sinφ sinα

y = r cosφ sin α + r sin φ cos α

x = x₁ cosα – y₁sinα)

y = x₁ sin α + y₁ cos α)

r cosφ = x₁

r sinφ = y₁

Уравнения линий на плоскости:

1. В декартовой системе F(x; y) = 0

2. Параметрические

3. В полярных координатах F (r; φ) = 0

4. Векторным уравнением , где t – скалярный переменный параметр

28. Уравнение прямой на плоскости, все виды и переход от одного к другому. Основные задачи.

Векторное: (r₂ – r₁) N = 0, r1 – радиус-вектор. начала напрвавл вектора; r2 – радиус-вектор конца напрвавл. вектора; N – нормаль

С вектором нормали и точкой A(x-x₀)+B(y-y₀)=0; (А;В)–координаты вектора нормали, (х;у)–точки

Общее: Ах+Ву+С = 0

Каноническое: (m;n) – координаты направляющего вектора

Через 2 точки:

Уравнение в отрезках: a, b – отрезки, отсекаемые прямой на соответствующих осях

Нормальное уравнение xcosα + ycosβ – p = 0 p – расстояние от прямой до начала координат, cosα, cosβ - направляющие косинусы

Уравнение с угловым коэффициентом: y = kx+b; k=tgφ=-A/B; b = -C/B

Параметрическое уравнения прямой.

Угол между прямыми:

Расстояние от точки до прямой:

Условие параллельности: А1/A2 =B1/B2; m1/m2=n1/n2

Условие перпендикулярности: A1A2+B1B2=0; m1m2+n1n2=0

Угол между прямыми: cosϴ = (A₁A₂+B₁B₂)/sqrt(A₁²+B₁²)*sqrt(A₂²+B₂²)

cosϴ = (m₁m₂+n₁n₂)/sqrt(m₁²+n₁²)*sqrt(m₂²+n₂²)

tgϴ = (k₁-k₂)/(1+k₁k₂)

29. Эллипс. Вывод канонического уравнения и его свойства.

Пусть М (х;у) – произвольная точка эллипса. 2а – большая полуось, 2с – между фокусами

Т.к. MF₁ + MF₂ = 2a

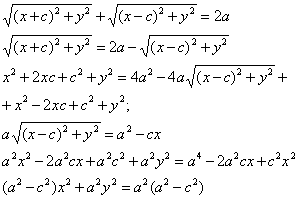
Т.к.

То получаем

Или

ε = с/a – эксцентриситет. ε = 0 => окружность; ε = 1 => отрезок

30. Гипербола. Вывод канонического уравнения и ее свойства.

Пусть M(x;y) – произвольная точка гиперболы. Тогда согласно определению гиперболы |MF₁ – MF₂|=2a или MF₁ – MF₂=±2a,

с² = а² + b²

асимптоты: y = +- bx/a

a – действительная полуось

b – мнимая полуось

31. Парабола. Вывод канонического уравнения и ее свойства.

Пусть M(x;y) – произвольная точка M с F. Проведем отрезок MN перпендикулярно директрисе. Согласно определению MF=MN.

Фокус F (p/2; 0)

Директриса l: x=p/2

32. Общее уравнение кривой второго порядка. Приведение кривой второго порядка к каноническому виду.

Ax²+2Bxy+Cy²+2Dx+2Ey+F = 0 – общее уравнение кривой второго порядка

Приведение кривой второго порядка к каноническому виду осуществляется путем поворота осей координат относительно (0;0) и их параллельного переноса

Перенос: 0₁ (a; b) – начало координат в новой системе

M (x; y) – точка в старой системе

M (x₁; y₁) – точка в новой системе

Очевидно, что x₁ = x - a; y₁ = y – b. Чтобы узнать величину a и b, нужно выделить полные квадраты в общем уравнении кривой

Поворот: α – угол поворота; φ – угол между радиус-векторами точки M и новой осью координат

x = r_m*cos(φ+α)

y = r_m*sin(φ+α)

x = r (cosφ cosα – sinφ sinα)

y = r (cosφ sin α + sin φ cos α)

x = r cosφ cosα – r sinφ sinα

y = r cosφ sin α + r sin φ cos α

x = x₁ cosα – y₁sinα)

y = x₁ sin α + y₁ cos α)

r cosφ = x₁

r sinφ = y₁