16. Скалярное произведение. Выражение скалярного произведения через координаты. Приложения скалярного произведения.

Скалярное произведение двух векторов – это число, равное произведению их длин на косинус угла между ними.

Свойства скалярного произведения:

Выражение скалярного произведения через координаты . Скалярное произведение векторов равно сумме попарных произведений их одноименных координат

Приложения:

Угол между векторами Условие перпендикулярности векторов – скалярное произведение векторов равно нулю

Проекция вектора на заданное направление

Работа постоянной силы при прямолинейном перемещении ее точки приложения равна скалярному произведению вектора силы на вектор перемещения

17. Векторное произведение. Выражение векторного произведения через координаты. Приложения векторного произведения.

Векторным произведением векторов а и b называется вектор с, который перпендикулярен векторам а и b, имеет длину, численно равную площади параллелограмма, построенного на векторах а и b, вектора а, b, с образуют правую тройку

Свойства векторного произведения:

При перестановке сомножителей векторное произведение меняет знак

k(a x b) = (ka) x b = a x (kb), где a и b – векторы, k – константа (векторное произведение обладает сочетательным свойством относительно скалярной величины)

Два ненулевых вектора коллинеарны только тогда, когда их векторное произведение равно нулевому вектору

Векторное произведение обладает распределительным свойством (a+b) x c = a x c+b x c

Выражение векторного произведения через координаты

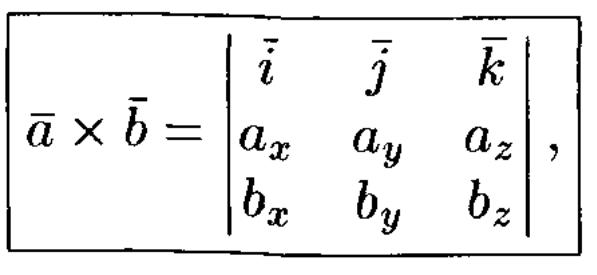
Приложения векторного произведения:

Нахождение площади параллелограмма

18. Определение смешанного произведения, его геометрический смысл. Выражение смешанного произведения через координаты. Приложения смешанного произведения.

Смешанное произведение векторов а, b и с – это произведение, составленное следующим образом: (а х b) с. Первые два вектора перемножаются векторно, а их результат скалярно на третий вектор.

Смешанное произведение трех векторов – это число, равное объему параллелограмма, построенного на этих векторах, взятое со знаком «+», если они образуют правую тройку, и «-», если левую

Свойства смешанного произведения:

Смешанное произведение не меняется при циклической перестановке его сомножителей

Не меняется при перемене местами знаков векторного и скалярного умножения (а х b) с = а (b x c)

Смешанное произведение меняет знак при перестановке любых двух векторов-сомножителей

Смешанное произведение трех векторов равно нулю только тогда, когда они компланарны

Выражение смешанного произведения через координаты

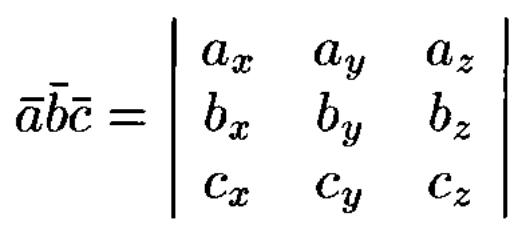
Приложения смешанного произведения:

Определение взаимной ориентации векторов в пространстве: abc>0 – правая тройка abc<0 – левая

Установление компланарности векторов: если abc=0, то a, b, c – векторы

Объем параллелепипеда, построенного на векторах a, b, c, вычисляется как

Объем треугольной пирамиды, построенной на этих векторах, равен

19. - Мерный вектор. Линейные операции над векторами. Скалярное произведение. Длина.

Линейные операции над векторами:

Умножение на число. Вектор, умноженный на число имеет длину, равную произведению исходной длины на это число, сонаправлен с исходным вектором, если число положительное, противоположно направлен исходному, если число отрицательное

Сложение векторов. Сумма векторов – вектор, соединяющий начало одного вектора с концом другого, если они второй вектор отложен от конца первого. Каждая координата суммы векторов есть сумма соответствующей координаты всех суммируемых векторов. Разность векторов – вектор, соединяющий конец вычитаемого вектора с концом уменьшаемого, если эти вектора отложены от одной точки. Сумма и разность векторов лежат на разных диагоналях параллелограмма, построенного на этих векторах

Свойства линейных операций над векторами:

Скалярное произведение двух векторов – это число, равное произведению их длин на косинус угла между ними.

Свойства скалярного произведения:

Выражение скалярного произведения через координаты. Скалярное произведение векторов равно сумме попарных произведений их одноименных координат

Длина: