11. Системы линейных однородных уравнений. Необходимое и достаточное условие существования ненулевых решений.

12. Фундаментальная система решений однородной системы линейных уравнений.

Фундаментальная система решений – совокупность линейно независимых решений однородной системы уравнений, число решений зависит от числа свободных переменных

Пусть r – ранг матрицы, тогда:

• Если r = n, где n — число переменных системы, то существует только тривиальное решение;

• Если r < n, то существует (n – r) линейно независимых решений рассматриваемой системы:  , причём её общее решение имеет вид: 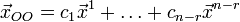 , где   — некоторые константы.

13. Неоднородные системы линейных уравнений.

Неоднородная система линейных уравнений – система, в которой свободные члены не равны нулю

Пусть ранг основной матрицы равен рангу расширенной матрицы (т.е. система совместна), тогда:

• Если r = n, где n — число переменных системы (2), то решение (2) существует и оно единственно;

• Если r < n, то общее решение находится как сумма общего решения соответствующей однородной системы и частного решения системы.

14. Векторы. Линейная зависимость и независимость векторов. Базис и координаты в трехмерном пространстве.

Система векторов линейно независима, если их линейная комбинация равна нулю только в том случае, когда все коэффициенты равны нулю, и линейно зависима тогда, когда линейная комбинация равна нулю, и при этом существует хотя бы 1 отличный от нуля коэффициент.

Если система векторов линейно зависима, то хотя бы один вектор системы можно представить в виде линейной комбинации остальных.

Линейная комбинация векторов: с₁а₁+с₂а₂+…+с_na_n. а1, а2 – вектора, с1, с2 – коэффициенты

Базис – совокупность линейно независимых векторов некоторого пространства, при условии, что количество векторов совпадает с размерностью данного пространства.

В трехмерном пространстве базис образуют три некомпланарных вектора. Любой вектор в пространстве можно представить в виде линейной комбинации базисных векторов. Разложение любого вектора в конкретном базисе единственно.

i, j, k – ортонормированный базис векторов, образующих правую тройку (вектора попарно перпендикулярны, длина каждого равна 1, тройка векторов называется правой, если при наблюдении с конца третьего вектора кратчайший путь от первого ко второму видится против часовой стрелки)

Координаты вектора в базисе – коэффициенты его разложения по данному базису

15. Проекция вектора на ось. Разложение вектора по ортам координатных осей. Направляющие косинусы.

Ось – направленная прямая

Проекция вектора на ось:

Если вектор лежит на оси, то проекцией вектора на ось называется число, равное длине вектора, взятое со знаком «+», если направление вектора и оси совпадают, и «–» если нет.

Если вектор не лежит на оси, то а’ – компонента вектора а на оси. Проекция компоненты = проекции вектора. Проекция вектора на ось равна произведению модуля этого вектора на косинус угла между вектором и осью.

Проекция суммы векторов на одну ось равна сумме их проекций на эту ось

При умножении вектора на число, его проекция на ось также умножается на это число

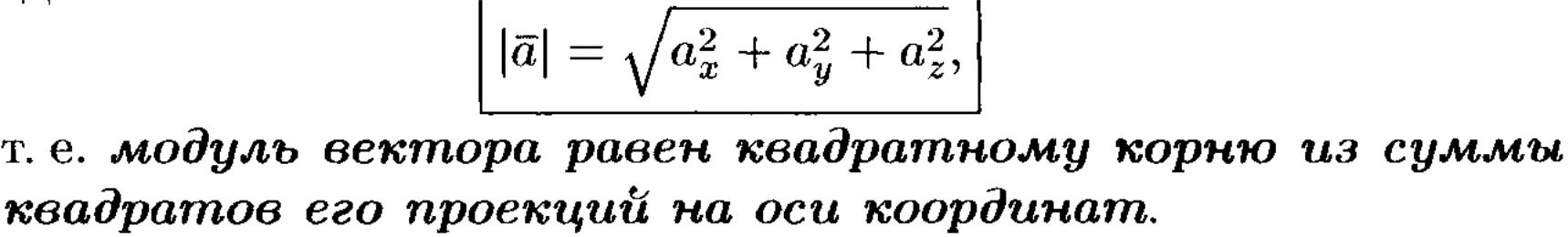
Направляющие косинусы – это косинусы углов, которые образует вектор с координатными осями.