5. Невырожденная матрица. Обратная матрица.

Квадратная матрица называется невырожденной, если ее определитель не равен нулю.

Матрица В является обратной матрице А, если АВ=ВА=Е. Матрица, обратная матрице А обозначается А^-1. Любая невырожденная матрица имеет обратную.

Свойства обратной матрицы:

1)Определитель обратной матрицы равен единице, деленой на определитель исходной матрицы

2)Обратная матрица произведения равна произведению обратных матриц

3)Транспонированная обратная матрица равна обратной матрице для транспонированной исходной

6. Ранг матрицы.

Ранг матрицы – это наибольший порядок отличного от нуля минора данной матрицы. Например, если среди миноров третьего порядка есть ненулевые, а все миноры четвертого порядка равны нулю, то ранг матрицы равен трем.

7. Линейная независимость рядов матрицы. Теорема о ранге матрицы.

c₁A₁ + c₂A₂ + … + c_iA_i - линейная комбинация матрицы, где A_i – i-ый ряд матрицы, c_i – коэффициент (константа).

Ряды называются линейно независимыми, если их линейная комбинация равна нулю только в том случае, когда все коэффициенты с_i = 0.

Теорема о ранге матрицы: ранг матрицы равен максимальному числу линейно независимых столбцов

8. Системы линейных уравнений. Основные понятия. Метод обратной матрицы.

Система называется линейной, если все неизвестные в ней входят только в первой степени.

Совместная система – имеющая хотя бы одно решение

Несовметстная система – система, не имеющая решений

Совместные системы бывают определенными (имеют единственное решение) и неопределенными (имеют множество решений).

В неопределенных системах каждое их решение называется частным, совокупность частных решений – общее решение.

Частное решение – любой вектор Х, который при подстановке в исходную систему обращает все ее уравнения в верные равенства.

Решить систему – значит выяснить, совместна ли она, если совместна, найти ее общее решение

Эквивалентные системы – системы, имеющие одно и то же решение

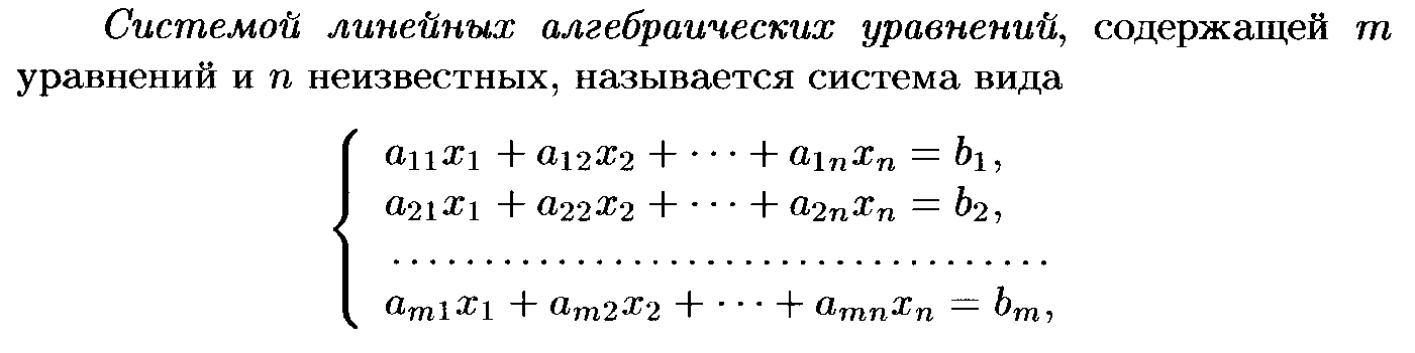
Система линейных уравнений называется однородной, если все свободные члены равны нулю. Однородная система всегда совместна, т.к. ситуация, когда все неизвестные равны нулю, является ее решением. Такое решение называется нулевым или тривиальным ( )

9. Решение невырожденных линейных систем. Формулы Крамера.

Основная матрица А системы квадратная, ее определитель называется определителем системы, если определитель системы отличен от нуля, то система невырожденная.

Умножим обе части уравнения (матричной формы) на А^-1, получим А * А^-1 * Х = А^-1 * В,

А * А^-1 = Е и Е * Х = Х, следовательно Х = А^-1 * В

10. Решение системы линейных уравнений методом Гаусса. Теорема Кронекера-Капелли.

Метод Гаусса:

1. Прямой ход. Матрица коэффициентов (основная) с помощью элементарных преобразований приводится к ступенчатому виду (она станет треугольной, если система имеет 1 решение, или трапецеидальной, если система имеет бесконечно много решений)

2. Анализ системы на совместность, определенность, определение базисных (их число равно рангу матрицы) и свободных (их число равно разности общего числа неизвестных и ранга матрицы) переменных. Базисный минор должен быть отличен от нуля.

3. Обратный ход. Решение ступенчатой системы уравнений, путем выражения неизвестных через другие неизвестные и подстановки их в другие уравнения системы.

При этом возможны 2 случая:

1.Ранг матрицы, совпадающий с рангом расширенной матрицы, равен числу неизвестных в системе, тогда система имеет единственное решение

2.Ранг матрицы меньше числа неизвестных, тогда система имеет бесконечно много решений