Вопрос 27

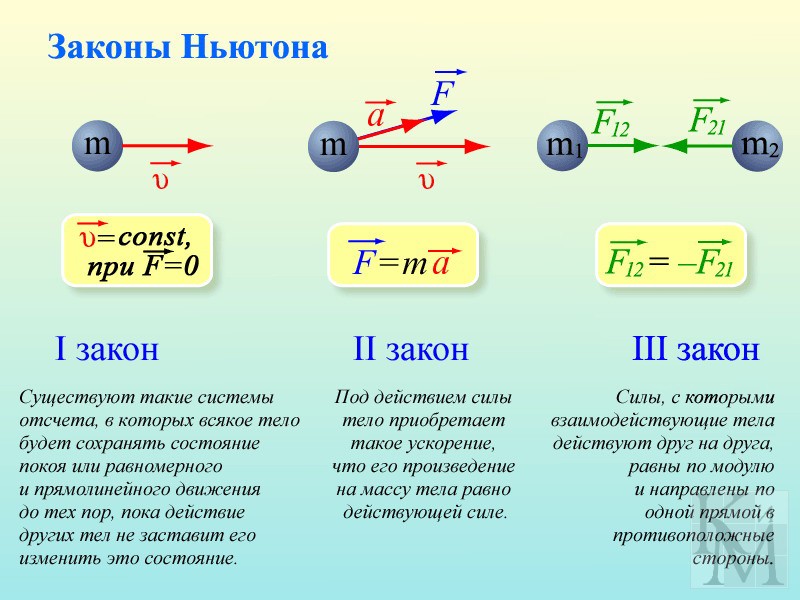
Динамикой называется раздел механики, в котором изучается движение материальных тел в зависимости от действующих на них сил.

Силы в динамике переменные и могут зависеть от времени, положения тела и от его скорости.

Вопрос 28

Вопрос 29

Уравнениями Лагранжа второго рода называют дифференциальные уравнения движения механической системы, получаемые при применении лагранжева формализма.

[править]Вид уравнений

Если голономная механическая система описывается лагранжианом   (  — обобщённые координаты, t — время, точкой обозначено дифференцирование по времени) и в системе действуют только потенциальные силы, то уравнения Лагранжа второго рода имеют вид

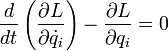
где i = 1, 2, … n (n — число степеней свободы механической системы).

Если в системе действуют непотенциальные силы (например, силы трения), уравнения Лагранжа второго рода имеют вид

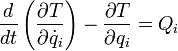
где   — кинетическая энергия системы,   — обобщённая сила.

Вопрос 30

Из основного уравнения динамики вращательного движения следует, что

Для замкнутой (изолированной) системы результирующий вектор момента   всех внешних сил, действующих на тело, равен нулю и

или

Это утверждение представляет собой содержание закона сохранения момента количества движения: и формулируется следующим образом: если результирующий момент всех внешних сил относительно неподвижной осивращения тела равен нулю, то момент импульса относительно этой оси не изменяется в процессе движения. Этот закон может быть обобщен на любую незамкнутую систему тел, если результирующий момент всех внешних сил, приложенных к системе, относительно какой-либо неподвижной оси тождественно равен нулю, то момент импульса системы относительно той же оси не изменяется с течением времени.

Вопрос 31

17.2. Приведение системы сил инерции твердого тела к простейшему виду

По теореме Пуансо систему сил инерции, приложенных к точкам твердого тела, в общем случае можно заменить силой и парой сил. Сила приложена в центре приведения и равна главному вектору сил инерции, момент пары равен главному моменту сил инерции относительно центра приведения. 

 

Поскольку  ,  , применяя теорему о движении центра масс и теорему об изменении кинетического момента, находим:   ,       .  Здесь за центр приведения   принята произвольная неподвижная точка в инерциальной системе отсчета.  Обычно за центр приведения выбирается центр масс механической системы.

 

Тогда с учетом теоремы об изменении кинетического момента в поступательно движущейся с центром масс системе отсчета   ,     .

Вопрос 14

Потенциальная энергия   в поле тяготения Земли вблизи поверхности приближённо выражается формулой:

Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного ивращательного движения.

Рассмотрим систему, состоящую из одной частицы, и запишем второй закон Ньютона:

Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системыможет быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципом сохранения энергии.