1 вопрос

 Динамика- раздел теоретической механики, изучающий движение материальных объектов с учетом сил, вызывающих это движение. В динамике изучаются механические движения материальных объектов под действием сил.  Простейшим материальным объектом является материальная точка.

Материальная точка это модель материального тела любой формы, размерами которого можно пренебречь и принять за геометрическую точку, имеющую определенную массу. Более сложные материальные объекты – механические системы и твердые тела, состоят из набора материальных точек.

Движение материальных объектов всегда происходит в пространстве относительно определенной системы отсчета и во времени. Пространство считается трехмерным эвклидовым пространством, свойства которого не зависят от движущихся в нем материальных объектов.

Время в классической механике не связано с пространством и движением материальных объектов. Во всех системах отсчета движущихся друг относительно друга оно протекает одинаково.

Две основные задачи динамики:

1.по заданному движению точки определить силы, вызывающие это движение.

2. по заданным силам определить движение точки.

Законы Ньютона

Классическая динамика основана на трёх основных законах Ньютона:

• 1-й: Существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или их действие скомпенсировано.

• 2-й: В инерциальной системе отсчета сумма всех сил, действующих на тело, равна произведению массы этого тела на векторное ускорение этого же тела (действие на тело силы, проявляется в сообщении ему ускорения).

В наиболее общем случае, который описывает также движение тела с изменяющейся массой (например, реактивное движение), 2-й закон Ньютона принято записывать следующим образом:

,

где   — импульс тела. Таким образом, сила характеризует быстроту изменения импульса.

• 3-й: Тела действуют друг на друга силами равными по модулю и противоположными по направлению

Если при этом рассматриваются взаимодействующие материальные точки, то обе эти силы действуют вдоль прямой, их соединяющей. Это приводит к тому, что суммарный момент импульса системы состоящей из двух материальных точек в процессе взаимодействия остается неизменным. Таким образом, из второго и третьего законов Ньютона могут быть получены законы сохранения импульса и момента импульса

2 Вопрос

Теорема об изменении количества движения. Если удерживающие и односторонние связи, наложенные на систему, идеальны и допускают поступательный сдвиг всех точек системы как твердого тела вдоль какого-нибудь направления   постоянного во времени, то проекция количества движения системы на это направление   является абсолютно непрерывной функцией и скорость ее изменения равна  , т.е. равна суммарной проекции на это направление вектора активных сил.

              

И́мпульс си́лы — это векторная физическая величина, равная произведению силы на время её действия, мера воздействия силы на тело за данный промежуток времени (в поступательном движении).

За конечный промежуток времени эта величина равна определённому интегралу от элемен­тарного импульса силы, где пределами интегрирования являются моменты начала и конца промежутка времени действия силы. В случае одновременного действия нескольких сил сумма их импульсов равна импульсу их равнодействующей за то же время.

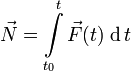
Количество движения механической системы – векторная величина  , равняющаяся геометрической сумме (главному вектору) количества движения всех точек системы.или количество движения системы равняется произведению массы всей системы на скорость ее центра масс     Когда тело (или система) движется так, что ее центр масс неподвижен , то количество движения тела равняется нулю   (пример, вращение тела вокруг неподвижной оси, которая проходит через центр масс тела).      Если движение тела сложное, то   не будет характеризовать вращательную часть движения при вращении вокруг центра масс. Т.е., количество движения характеризует только поступательное движение системы (вместе с центром масс).

3 Вопрос

Рассмотрим движение свободной материальной точки в инерциальной системе отсчёта в декартовых координатах. Из 2-го закона Ньютона:

   ,   , 

причём, Fx, Fy, Fz – могут зависеть от координат, первых производных, времени:   .

Вопрос 4

Закон сохранения количества движения системы.

1. Если сумма всех внешних сил, действующих на систему, равняется нулю, то вектор количества движения системы будет постоянным по направлению и по модулю.      

2. Если сумма проекций всех действующих внешних сил на любую произвольную ось равняется нулю, то проекция количества движения на эту ось является величиной постоянной.

      Законы сохранения свидетельствуют, что внутренние силы не могут изменить суммарное количество движения системы.

Две задачи динамики точки.

   Первая задача динамики (прямая).    Дано:  масса точки, уравнение ее движения    Определить: модуль и направление равнодействующей сил, приложенных к точке.   Решение первой задачи динамики проводится методом двойного дифференцирования уравнений движения по времени.    Вторая задача динамики (обратная, основная).    Дано:масса точки, силы, действующие на точку, начальное положение,начальная скорость     Определить: закон движения  ,  ,     Решение второй задачи динамики осуществляется методом двойного интегрирования  по времени дифференциальных уравнений при известных начальных условиях.

Скорость тела в любой момент времени v_y = ± v_oy ± g_yt  Перемещение тела s_y = ± v_oyt ± (g_yt²) / 2 Координаты тела (высота тела) y = h = h₀ ± v_oyt ± (g_yt²) / 2  Скорость тела в любой точке пути v_y² = v_oy² + 2g_y(h - h₀)