
- •Множества. Понятие множества, элемента, способы задания множеств. Числовые множества. Соотношения между множествами. Подмножества.
- •Пересечение множеств и его свойства.
- •Объединение множеств и его свойства.
- •Дистрибутивные законы, связывающие объединение и пересечение. Иллюстрация, док-во рассуждением и таблицей.
- •Разность множеств. Дополнение к подмножеству. Свойства дополнения. Иллюстрация, доказательство.
- •Разбиение множества на классы. Правила классификации. Разбиение на классы с помощью одного, двух свойств, трех свойств.
- •Декартово произведение множеств. Способы задания декартово произведения.
- •Иллюстрация декартового произведения числовых множеств на координатной плоскости.
- •Свойства декартова произведения: дистрибутивность декартова произведения относительно объединения, пересечения и разности множеств. Иллюстрация, доказательство.
- •11. Размещения с повторениями. Число размещений с повторениями. Вывод формулы.
- •12. Размещение без повторений и их число. Вывод формулы. Перестановки. Формула для подсчета числа перестановок.
- •13. Сочетания без повторений. Вывод формулы.
- •14. Комбинаторные задачи в начальной школе и методы их решения.
- •16. Конъюнция высказываний и ее свойства. Конъюнкция предикатов и ее множество истинности. Примеры.
- •17. Дизъюнкция высказываний и её свойства. Дизъюнкция предикатов и ее множество истинности. Примеры.
- •18. Дистрибутивные законы, связывающие конъюнкцию и дизъюнкцию. Док-во с помощью таблицы.
- •19. Отрицание высказываний и его свойства. Отрицание предикатов и его множества истинности. Примеры.
- •20. Отрицание конъюнкции и дизъюнкции.
- •21. Импликация высказываний. Связь импликации с дизъюнкцией. Отрицание импликации.
- •22. Виды импликаций и их связь. Док-во равносильности прямой импликации и обратной противоположной
- •23. Множество истинности импликации предикатов. Случай логического следования. Необходимые и достаточные условия.
- •25. Кванторы. Установление истинности высказываний с кванторами. Отрицание высказываний, содержащих кванторы.
- •26. Строение и виды теорем
19. Отрицание высказываний и его свойства. Отрицание предикатов и его множества истинности. Примеры.
Отрицание высказываний строится с помощью частицей «не»
Отрицанием высказывания А называется высказывание «не А»,которое ложно,когда А-истина, и истина,когда А-ложно.
Отрицание конъюнкции равно дизъюнкции отрицаний.
Отрицание – логическая связка, с помощью которой из данного высказывания получается новое, причем, если исходное высказывание истинно, его отрицание будет ложным, и наоборот. Отрицательное высказывание состоит из исходного высказывания и отрицания, выражаемого обычно словами "не", "неверно, что". Отрицательное высказывание является, таким образом, сложным высказыванием: оно включает в качестве своей части отличное от него высказывание. Например, отрицанием высказывания "10 – четное число" является высказывание "10 не есть четное число" (или: "Неверно, что 10 есть четное число").
Отрицанием
предиката A (x) называется
предикат  множество
истинности T которого
является дополнением к множеству T1,
то есть T = X \ T1
множество
истинности T которого
является дополнением к множеству T1,
то есть T = X \ T1
20. Отрицание конъюнкции и дизъюнкции.
Отрицание конъюнкции равно дизъюнкции отрицания и наоборот.
21. Импликация высказываний. Связь импликации с дизъюнкцией. Отрицание импликации.
Импликацией высказываний А и В называется высказывание «если А, то В», которое ложно в одном случае, когда А истинно, а В ложно, и истинно во всех остальных случаях. Импликацию высказываний А и В обозначают А В и читают: « Из а следует В» или «если А, то В». высказывание А называют условием импликации, высказывание В – её заключением. Например, в импликации {если x – число натуральное, то оно целое} предикат B (x) = {x – число целое} логически следует из предиката A (x) = {x – число натуральное}. Следовательно, предикат B (x) является необходимым условием для предиката A (x), а предикат A (x) – достаточным для B (x). Используя эти термины, импликацию {если число x натуральное, то оно целое} можно выразить так:
Для того чтобы число x было натуральным, необходимо, чтобы оно было целым.
Для того чтобы число x было целым, достаточно, чтобы оно было натуральным.
если точно указано, чему равны x и y, каждое из сформулированных утверждений превращается в высказывание – для одних пар (x, y) истинное, для других ложное. Множество всех пар чисел (x, y), для которых данный двухместный предикат есть истинное высказывание, называется множеством его истинности.
Приведем примеры высказываний, получающихся из указанных предложений при конкретных значениях x и y:
A (1; 3) = {1 < 3} – истинное высказывание,
A (2; 2) = {2 < 2} – ложное высказывание,
A (5; 4) = {5 < 4} – ложное высказывание,
B (1; 3) = {1 + 3 = 10} – ложное высказывание,
B (8; 2) = {8 + 2 = 10} – истинное высказывание и т.д.
Импликация
высказываний связана с дизъюнкцией:
А
В
= отрицание А v В. Отсюда следует, что
отрицание (А
В)
= А ^ отрицание В. Импликацию можно
выразить через дизъюнкцию и
отрицание: А  В
=
В
= 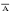 v
В.
v
В.
22. Виды импликаций и их связь. Док-во равносильности прямой импликации и обратной противоположной
Выделяют 4 вида импликации: А В – прямая, В А – обратная, отрицание А отрицание В – противоположная, отрицание В отрицание а – обратная противоположной. Прямая импликация и обратная противоположной равны. Докажем с помощью таблицы.
А |
В |
А В |
-А |
-В |
-В А |
И |
И |
И |
Л |
Л |
И |
И |
Л |
Л |
Л |
И |
Л |
Л |
И |
И |
И |
Л |
И |
Л |
Л |
И |
И |
И |
И |
В 3м и 6м столбике значение истинности одинаковое, значит равенство доказано.
