11. Размещения с повторениями. Число размещений с повторениями. Вывод формулы.

Размещением с повторениями из m по k называется кортеж длины k, составленный из элементов множества, в котором m элементов. Кортежом называется {х1,х2...хn} их число называется длиной кортяжа. Число размещений с повторениями обозначают и подсчитывают по формуле 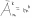. В размещении с повторениями все элементы могут повторяться, порядок элементов имеет значение, числа m и k произвольные. Примером размещения с повторениями являются многозначные числа или слова русского языка. Подсчитаем кол-во размещений с повторениями из m по k. На первое место в картеж элемент можно взять m-способами. на второе место – m-способов. И т.д. а на k место – m способов. По правила произв-я всего будет m в степени k.

12. Размещение без повторений и их число. Вывод формулы. Перестановки. Формула для подсчета числа перестановок.

Размещением без повторений из m элементов по k называется упорядоченное подмножество, содержащее k элементов, которые берутся из множества, содержащего m-элементов. Элементы не повторяются. Порядок элементов имеют значение. Всегда m больше k (допускается случай равенства m=k). Пусть дано мн-во из m-элементов.Составить упорядоченное подмножество из k элементов. На 1 место можно выбрать m способ. На 2 место- (m-1) способ. На 3 место- (m-2) способ. На 4 Место- (m-3) способ. На 5 место- (m-k +1) способ. Число размещений без повторений будет равно m.(m-1)(m-2)(m-3)(m-k+1). Перестановки без повторения являются частым случаем размещения без повторения. Если в размещении без повторений из m элементов участвуют k элементов, то в перестановке участвуют все m-элементы. Перестановкой из m-элементов, называется упорядоченное мн-во из m элементов. Число перестановок обозначается Рm. 1е место – m способов, 2 е место (m-1) способ, 3 е место (m-2) способов и т.д. по правилу произв-я будет всего Pm=m*(m-1)(m-2)…2*1. Произведение натуральных чисел от одного до m, называется факториалом и обозначается m! 3!=1*2*3=6.

13. Сочетания без повторений. Вывод формулы.

Иногда требуется из m-элементов составить комбинацию из k-элементов, причем порядок не имеет значения. Например: из 25 студентов пять отправить на конференцию. Такие комбинации называются сочетаниями из m элементов по k. Сочетаниям из m элементов по k, называется подмножество, содержащее k элементов, сост из элементов мн-ва, в котором m элементов. Сравнивая это определение с размещение без повторений, мы видим, что ушло слово упорядоченное подмножество, т.е. в сочетании порядок не имеет значения. Отсюда, получим вывод формулы числа сочетаний без повторений. С (верху k, внизу m). Упорядоченных подмножеств будет больше во столько раз, сколькими способами можно переставлять эти k элементы.

14. Комбинаторные задачи в начальной школе и методы их решения.

Существуют следующие методы решения комбинаторных задач: Метод перебора (подбираются задачи на развитие мышления); Табличный метод (здесь все условия вносятся в таблицу, возникает решение); Дерево вариантов (дети получают начальные знания о графах)

Методы решения комбинаторных задач вводятся по нарастающей траектории от простого к сложному. В 1–2 классе решаются задачи с помощью перебора и таблиц, а в 3–4 с помощью построения дерева вариантов и графов, тем самым позволяя в основной школе при изучении некоторых тем теории вероятности использовать знакомые понятия и способы решения.

Комбинаторные задачи являются средством:

1. Реализации методической концепции, выражающей необходимость целенаправленного и систематического формирования приемов умственной деятельности в процессе усвоения программного содержания.

2. Овладения способом моделирования на доступном для младших школьников уровне.

3. Расширения у учащихся представлений о различных видах математических задач и способах их решения (перебор, таблицы, дерево вариантов)

4. Развития таких свойств мышления как гибкость, вариативность, креативность.

В конце изучения курса математики в начальной школе учащиеся владеют способами решения комбинаторных задач, умеют составлять математически

Комбинаторные задачи, составленные на жизненном материале, помогают младшим школьникам лучше ориентироваться в окружающем мире, учат рассматривать все имеющиеся возможности и делать оптимальный выбор. Рассмотрим одну из них. Учащимся предлагается следующая проблема: « У тебя 60 рублей. Родители отпустили тебя в парк покататься на каруселях. Предлагаются следующие расценки. Вход в парк – 5 рублей. «Колесо обозрения” – 10 рублей. «Сюрприз – 35 рублей.. «Американские горки” – 45 рублей. «Комната смеха” – 25 рублей. Какой выбор ты сделаешь, если ни один из аттракционов нельзя посетить дважды?. Ребенок, анализируя задачу, приходит к построению такой математической модели:. Реальность – постановка условий – составление возможных вариантов – выбор варианта. Тем самым ребенок ставит следующие условия:. Ребенок должен войти в парк, потратить 5 рублей. Стоимость всех посещенных аттракционов должна быть меньше, либо равна 55.Ни один из аттракционов не должен быть посещен дважды.

15. Высказывания и высказывательные формы. Логические связки, виды высказываний.

Отрицание высказываний строится с помощью частицей «не»

Отрицанием высказывания А называется высказывание «не А»,которое ложно,когда А-истина, и истина,когда А-ложно.

Отрицание конъюнкции равно дизъюнкции отрицаний.

Основным понятием математической логики является высказывание – любое повествовательное предложение, про которое известно, является оно истинным или ложным. Высказывания могут быть описаны либо с помощью слов, либо некоторых символов. Например, являются высказываниями:

а) «сумма чисел 2 и 5 равна 7» (истинное высказывание),

б) «2 + 5 = 7» — предыдущее высказывание, записанное с помощью математических символов. Высказывательной формой или предикатом, называется предложение с одной или несколькими переменными, обращающееся в высказывание, если вмето переменных подставить их значения. Предложения, не являющиеся составными, называются элементарными. Соответственно, если можно судить об истинности или ложности таких предложений, то они будут называться простыми и составными высказываниями. Например, высказывание «число делится на три тогда и только тогда, когда сумма цифр этого числа делится на три» является составным высказыванием (оно является истинным и в математике известно как признак делимости числа на три).

С точки зрения грамматики различают простые и сложные предложения. Например, предложение «число 10 делится на 2 и на 5» является простым, хотя с точки зрения математической логики это – сложное высказывание, состоящее из двух простых высказываний «число 10 делится на 2», «число 10 делится на 5», полученное с помощью логической связки «и» ложные высказывания. Логические операции над высказываниями. Аналогично тому, как в алгебре чисел используются операции сложения, вычитания, умножения, деления, в алгебре высказываний вводятся специальные операции, которые имеют названия логического сложения (дизъюнкции), логического умножения (конъюнкции), отрицания, импликации и эквиваленции.

Импликация и эквиваленция. Логические рассуждения чаще всего имеют форму цепочки высказываний. Эти высказывания имеют условный характер, то есть, утверждают, что некоторое высказывание истинно при условии, что истинно другое высказывание. Например, «если два угла одного треугольника соответственно равны двум углам другого треугольника, то эти треугольники подобны». В общем виде такого рода высказывания записываются следующим образом «если А, то В» и называются импликацией. Высказывание А в этом случае называют условием, а высказывание В –заключением.

Определение. Импликацией высказываний А и В называют высказывание   (читается «если А, то В»), ложное лишь в случае, когда А истинно, а В – ложно.

Определение. Эквиваленцией  высказываний А и В называют высказывание   (читается «А тогда и только тогда, когда  В»), истинное, в том и только в том случае, когда оба эти высказывания истинны, или оба ложны.