1. Множества. Понятие множества, элемента, способы задания множеств. Числовые множества. Соотношения между множествами. Подмножества.

Понятие множества является неопределяемым понятием. Его смысл разъясняется на примерах. Можно говорить о множестве жителей города Саратова, о мн-ве домов на конкретной улице и т.д. Множества принято обозначать большими латинскими буквами. Объекты, из которых состоит множество, называются его элементами. Если объект x является элементом множества А, то говорят, что х принадлежит А. Множество, в котором нет элемента, называется пустым. Множества можно задавать двумя способами: перечислением элементов множества (например, список класса определяет мн-во учеников класса, мн-во, не содержащее ни одного элемента называется пустым); описанием общего (характеристического) свойства, объединяющего элементы (например, запись А={x l x-житель саратова}, означает, что мн-во А состоит из жителей Саратова. Характеристическое св-во – это такое св-во, которым обладают все элементы данного мн-ва и не обладают никакие другие объекты. Множества, элементами которого являются числа, считаются числовыми. Для некоторых числовых множеств в математике приняты стандартные обозначения: N-мн-во натуральных чисел, Z-целых чисел, N или Z (с индексом 0) – мн-во целых неотрицательных чисел, Q- рациональных, R-действительных. Отношения между множествами.

1. Множество В является подмножеством А, если каждый элемент множества В принадлежит А.

2. Два множества равны, если они состоят из одних и тех же элементов.

3. Объединением двух множеств A и B называется множество, состоящее из тех элементов, которые принадлежат хотя бы одному из этих множеств.

4. Пересечением множеств A и B называется множество, в которое входят те и только те элементы, которые одновременно принадлежат множествам A и B.

5. Разностью двух множеств A и B называется такое множество, в которое входят все те элементы, которые принадлежат A и не принадлежат B

Множество В является подмножеством множества А, если каждый элемент множества В является также элементом множества А. Пустое множество является подмножеством любого множества. Само множество является подмножеством самого себя. Пустое мн-во и само мн-во называют несобственными подмножествами. Остальные подмножества множества А называются собственными. Если рассматривают лишь подмножества некоторого множества U, то U называют универсальным множеством.

2. Пересечение множеств и его свойства.

Пересечение множеств А и В называют множество, содержащее все элементы, которые принадлежат множеству А и множеству В. Пересечение множеств А и В обозначают А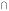 В. Таким образом, по определению А В={х x A и х В}.

Свойства:

1. А∩ В=В ∩ А ; переместительное св-во, коммутативное св-во

2. (А ∩В) ∩ С= А (В∩ С); сочетальное св-во,ассоциативное св-во

3. А ∩ U; U-универсальное мн-во,из кот. берутся все подмножества данной задачи.

4. А О=О; Пустое мн-во поглащающее в себя все элементы.

5. Если В А, то А В.