
- •1.Статистическое описание с позиции классической механики. Функция распределения.
- •Функция распределения.
- •2.Флуктуации аддитивных величин.
- •5. Каноническое распределение в классической статистической теории.
- •6. Термодинамика обратимых процессов.
- •7. Термодинамические функции и термодинамические равенства.
- •8.Классический идеальный одноатомный газ. Распределение Максвелла.
- •9. Классический расчет теплоемкости идеальной кристаллической решетки. Закон Дюлонга и Пти.
- •10. Большое каноническое распределение в классической статистической теории.
- •11.Статистическое описание с позиции квантовой механики.
- •12.Микроканоническое распределение в квантовой статистике.
- •13 И 14.Каноническое и большое каноническое распределения Гиббса в квантовой статистической теории.
- •15 И 16. Квантомеханическое описание колебаний кристаллической решетки. Теплоемкость кристаллической решетки.(при высоких и низких температурах).
- •17. Излучение абсолютно черного тела
- •1Ый Закон излучения Вина
- •2Й закон излучения Вина
- •18.Распределение Ферми-Дирака.
- •19.Идеальный ферми-газ. Плотность одночастичных стационарных состояний. Вычисление термодинамических величин с помощью плотности одночастичных стационарных состояний.
- •21) Вырожденный идеальный электронный газ. Химический потенциал и теплоемкость.
- •22) Электронная теплоемкость металлов.
- •23 И 24.Статистика равновесных носителей заряда в полупроводниках .Электронно-дырочная теплоемкость полупроводников.
- •25.Магнитные свойства вещества. Парамагнетизм газов и электронов проводимости в металлах и полупроводниках
- •Экспериментальные методы исследования поверхности Ферми
- •29. Бозе-Эйнштейна распределение
- •30. Вырожденный идеальный бозе-газ. Конденсация Бозе-Эйнштейна
- •32) Фазовые переходы. Классификация фазовых переходов.
- •33 И 34. Фазовые переходы второго рода. Модель Изинга. Теория Ландау фазовых переходов второго рода.
- •Модель Изинга.
Экспериментальные методы исследования поверхности Ферми
Форма поверхности Ферми определяет ряд свойств и важных характеристик металлов. Например, постоянная Холла в сильных полях в не скомпенсированных металлах в отсутствие открытых орбит при заданном направлении поля полностью определяется объемом k-пространства, заключенным внутри дырочной и электронной полостей поверхности Ферми. С формой поверхности Ферми тесно связаны кинетические коэффициенты металла, а также его равновесные и оптические свойства. Сопоставление с экспериментально определенной формой поверхности Ферми является критическим пунктом для оценки достоверности расчетов зонной структуры, базирующихся на тех или иных предположениях. Основы некоторых из экспериментальных методов будут изложены в этой лекции. Основным методом исследования поверхности Ферми, с помощью которого получена большая часть информации, является метод, основанный на эффекте де Гааза - ван Альфена и на родственных ему эффектах.
|
sD = s Bs = N |
(5.1) |
Соответственно (4.24), полная энергия уровней, которые полностью заполнены
U1 = |
(5.2) |
Полная энергия на электронов на частично занятом уровне s + 1 равна
U2 = c (s+1/2)(N-sD) |
(5.3) |
Полная энергия
U = U2 + U2 |
(5.4) |
|
|
(5.5) |
Осцилляции μ(1/В) и есть эффект dHvA. Из (4.20) видно, что осцилляции проходят через равные интервалы в 1/В, так что инкремент составляет
|
(5.6) |
где Se - согласно теории Онсагера, есть любая экстремальная замкнутая траектория, перпендикулярная В. Из измерений Δ(1/B) определяют соответствующую площадь Se, исходя из чего удается сконструировать форму и размеры поверхности Ферми.
|
Качественно выделение экстремальных орбит можно объяснить взаимным гашением фаз: вклады различных неэкстремальных орбит уничтожаются, однако, вблизи экстремумов фазы меняются медленно, фазы не гасятся полностью, и поэтому сигнал от этих орбит не исчезает.
Аналогичные (методу dHvA) методы. Среди других методов, аналогичных методу dHvA, следует, прежде всего отметить метод, базирующийся на эффекте Шубникова-де Гааза (1930), В этом методе наблюдаются осцилляции электрического сопротивления в магнитном поле.
Другие методы исследования поверхности Ферми. Дают менее однозначную геометрическую информацию по сравнению с эффектом dHvA, поэтому здесь приведено лишь очень краткая характеристика. Более полное изложение дано в АМ, Гл.14.
Магнитоакустический
эффект. Исследуют
затухание в металле звуковых волн,
распространяющихся ^ -но приложенному
постоянному магнитному полю В.
Поскольку ионы, несущие акустическую
волну, имеют заряд, то такая волна
генерирует электрическое поле с теми
же частотой, волновым вектором и
поляризацией. Благодаря электромагнитной
волне, электроны металла могут
взаимодействовать со звуковой волной
, усиливая или ослабляя ее. Если в
промежутке между столкновениями электрон
может совершать много оборотов в
магнитном поле, т.е.
c![]() >>1,
где
-
среднее время между столкновениями,
(сильное магнитное поле, низкие
температуры, очень чистый монокристалл),
то зависимость затухания звука от его
длины от его длины волны имеет осцилляторный
характер и может содержать информацию
о поперечных (по отношению кВ)
сечениях поверхности Ферми. Осцилляции
обусловлены условием резонанса в
поглощении или усилении акустической
волны, состоящим в кратности или
полукратности отношения диаметра lc орбиты
электрона вдоль распространения
акустической волны (т.е.
>>1,
где
-
среднее время между столкновениями,
(сильное магнитное поле, низкие
температуры, очень чистый монокристалл),
то зависимость затухания звука от его
длины от его длины волны имеет осцилляторный
характер и может содержать информацию
о поперечных (по отношению кВ)
сечениях поверхности Ферми. Осцилляции
обусловлены условием резонанса в
поглощении или усилении акустической
волны, состоящим в кратности или
полукратности отношения диаметра lc орбиты
электрона вдоль распространения
акустической волны (т.е. ![]() -но В)
и длиной волны
-но В)
и длиной волны ![]() .
Различают условие слабой связи (слабое
поглощение/усиление) и сильной связи
(сильное поглощение/усиление) электрона
с волной:
.
Различают условие слабой связи (слабое
поглощение/усиление) и сильной связи
(сильное поглощение/усиление) электрона
с волной:
Слабая связь - lc = n |
(5.7) |
Сильная связь - lc = (n+1/2) |
Нетрудно видеть, что в условиях слабой связи поглощение и усиление компенсируются в положительной и отрицательной полупериодах волны, чего не происходит в условиях сильной связи. Изменяя направление распространение звука и магнитного поля (с тем, чтобы могли проявиться различные экстремальные диаметры) иногда удается определить форму поверхности Ферми.
Аномальный скин-эффект.
Если
металлический образец облучается
микроволновым излучением с частотой
,
не слишком высокой, то это излучение
поглощается в слое толщиной ![]() 0,
равной
0,
равной
0 =
c/(2
|
(5.8) |
где - проводимость образца. Обычно 0 >> l - длины свободного пробега при достаточно малой частоте . Это т.н. "классическая" глубина скин-слоя. В случае 0 ~ l требуется более сложная теория, а режим 0 << lназывают предельно аномальным. В предельно аномальном режиме неприменимо представление об экспоненциальном затухании поля с глубиной. Глубина проникновения и коэффициент отражения в этом случае определяются некоторыми характеристиками поверхности Ферми, которые зависят от ориентации этой поверхности относительно реальной поверхности кристалла.
Циклотронный резонанс. Циклотронная масса.
|
Рассмотрим орбиту блоховского электрона с энергией Е в постоянном магнитном поле, лежащую в какой-либо плоскости, перпендикулярной магнитному полю, рис. 5.4. Для прохождения части орбиты в k-пространстве между значениями k1 и k2 требуется время
t
= t2 -
t1 = ![]() =
= ![]() =
2c/(eB)
=
2c/(eB)![]()
Градиент dE/dk ~ E/ k, где k направлено -но траектории (градиент dE/dk перпендикулярен изоэнергетической поверхности!), в отличие от dk, которое направлено вдоль нее. Т.е.
t ![]() 2c/(eB
E)
2c/(eB
E) ![]() kdk =
(
2c/eB)(
S1,2/
E).
kdk =
(
2c/eB)(
S1,2/
E).
При
E![]() 0
получаем для замкнутой траектории
период движения:
0
получаем для замкнутой траектории
период движения:
T = ( 2c/eB)[∂S(E,kz)/∂E] |
(5.9) |
Для свободных электронов:
T = 2 / c = (2 mc/ eB) |
(5.10а) |
Это же выражение может быть использовано для блоховских электронов:
T = (2 m*c/ eB), |
(5.10б) |
где
m* = ( 2/2 )[ S(E,kz)/ E] |
(5.11) |
- эффективная циклотронная масса электрона.
В описанном методе условие резонанса достигается в микроволновом диапазоне. При этих частотах имеет место аномальный режим поглощения, когда толщина скин-слоя становится часто меньше длины свободного пробега электронов и меньше размеров орбиты (в r-пространстве).
Эффект Азбеля-Канера.
|
1/B = n(2 / 2c )(1/[ S(E,kz)/ E]) |
(5.12) |
где 2 / TE.
Из условия резонанса (5.12) следует, что если изобразить поглощение энергии микроволнового поля как функцию от 1/В, то резонансные пики, отвечающие отдельному циклотронному периоду, будут располагаться через равные промежутки. Отсюда получаем S(E,kz)/ E. Проблема метода состоит в том, что несколько циклотронных масс могут давать вклад, что усложняет картину осцилляций.
Эффект Гантмахера (Гантмахер В.Ф., ЖЭТФ, 43 (1962) с.345)
|
При условии 0 < h < l в магнитном поле, возможны орбиты электронов, простирающиеся от скин-слоя от передней до задней поверхностей пластинки. Такие орбиты способны производить на задней поверхности электрический ток, который вызван приложенным снаружи электрическим УВЧ-полем на ее передней поверхности. Это приводит к генерации электромагнитного излучения с задней стороны пластинки. Поэтому в тех случаях, когда толщина h и величина магнитного поля В согласованы, должно наблюдаться резонансное возрастание прохождения электромагнитного излучения через пластинку. Как и в других методах эффективными оказываются электроны вблизи поверхности Ферми и с орбитами с экстремальными линейными размерами.
Зонная структура некоторых металлов
Щелочные металлы
Внутренние электроны конфигурации инертных газов, [Ne] - Na, [Ar] - K и т.д., сильно связаны с ядром, поэтому они дают низколежащие зоны, которые очень узки, полностью заполнены и описываются приближением сильной связи. Вне ионного кора находится один электрон проводимости. Если бы мы считали, что эти электроны ведут себя как свободные, то поверхность Ферми представляла собой сферу радиусом kF, которая определялась бы соотношением (1.23):
kF = (3 2n)1/3 = 0.62 (2 /a), |
(5.13а) |
Кратчайшее расстояние от центра зоны Бриллюэна до ее граней, ГN, (r-оцк (r) k-гцк) будет равно
ГN = (2 /a)[(1/22+(1/2)2+(0)]1/2 = 0.707 (2 /a) |
(5.13б) |
Т.о. сфера свободных электронов целиком лежит внутри 1-й з.Бр.. Ближе всего она подходит к ее границам в направлении ГN, а именно, kF/ГN = 0.877 (5.13в) Отличие поверхности Ферми от сферы свободных электронов мало - исчисляется долями процентов. Благодаря этой особенности, кинетические свойства щелочных металлов описываются хорошо в рамках теории свободных электронов Зоммерфельда.
Благородные металлы.
В отличие от щелочных металлов, в благородных металлах, помимо s-электрона на внешней атомной s-оболочке, имеются еще электроны на промежуточных d-орбиталях: Cu = [Ar]3d104s1, Ag = [Kr]4d105s1, Au = [Kr]4f145d106s1. Поэтому, если для щелочных металлов один s-электрон хорошо умещается в 1-ю з.Бр., то, например, для Cu требуется уже 6 зон для размещения 11-ти d- и s- электронов. [Как и в щелочных металлах, уровни электронов, принадлежащих заполненным инертно-подобным оболочкам, описывают в приближении сильной связи.] Расчеты показывают, что в Cu d-орбитали лежат в сравнительно узком интервале энергий от 2 до 5 эВ ниже EF, а s-орбиталь колеблется от 7 эВ выше EF до 9 эВ ниже EF. s-зона для всех k , за исключением тех, где она близко подходит к d-зонам, ведет себя как уровень свободных электронов. Измерения с помощью эффекта dHvA показывают, что у всех 3х благородных металлов поверхности Ферми очень похожи на сферу свободных электронов, но в направлении <111> в действительности они касаются граней зоны Бриллюэна (рис.5.1). Восемь "шеек" вытягиваются и касаются восьми шестиугольных граней зоны. В эффекте dHvA при В || направлению <111> имеются два четко выраженных периода колебаний (рис. 5.1). Они определяются экстремальными траекториями на "пузе" и на "шейке".
Двухвалентные металлы.
Внешняя электронная s-оболочка элементов 2й группы заполнена, см табл.5.1. Вследствие этого,
Таблица 5.1
Группа IIA: Be:1s22s2 гпу, ; Mg: [Ne]3s2 гпу; Ca: [Ar]4s2 гцк; Sr:[Kr]5s2 гцк; Ba[Xe]6s2 оцк;
Группа IIБ: Zr: [Ar]3d104s2 гпу; Cd: [Kr] 4d105s2 гпу; Hg [Xe] 4f145d106s2 р.э.;
верхняя s-зона также будет заполнена, и можно было бы ожидать, что эти элементы будут диэлектриками. В действительности они, хоть и не очень хорошие, но все же проводники. Это объясняется перекрытием самой верхней заполненной зоной с вышележащей зоной.
Присутствие или отсутствие заполненных d-зон играет в элементах 2й группы существенно меньшую роль по сравнению со щелочными и благородными металлами. Расчеты зонной структуры показывают, что в Zn и Cd d-зона полностью лежит ниже дна зоны проводимости, а в Hg она перекрывается с зоной проводимости лишь в очень узкой области вблизи ее дна. Различие свойств элементов 2й группы, в основном, связано с особенностями их структуры. В кубических 2х валентных металлах (Ca, Sr, Ba) объем сферы Ферми примерно равен объему 1й з.Бр.. Поэтому сфера Ферми пересекает грани зоны. Т.о. поверхность Ферми свободных электронов имеет довольно сложную структуру в 1-й з.Бр. и дырочные "карманы" во 2й зоне. Эффективный (псевдо) потенциал недостаточен чтобы сжать до нуля "карманы" 2й з.Бр. и заполнить т.о. все незанятые уровни в 1-й з.Бр.. Если бы это происходило, то эти элементы были бы диэлектриками. Очевидно, это не происходит, т.к. они являются металлами.
У ртути измерения показывают наличие электронных карманов во 2-й зоне и сложной протяженной структуры в 1й зоне Бриллюэна.
У гпу-металлов 2й группы (Be, Mg, Zn, Cd) поверхность Ферми представляет собой чрезвычайно сложную структуру, которую можно получить из сферы свободных электронов, содержащей по четыре уровня на каждую элементарную ячейку (в гпу - 2 атома на одну ячейку).

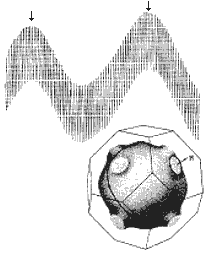 Рис.5.1.
Осцилляции де Гааза- ван Альфена (dHvA)
в серебре
Рис.5.1.
Осцилляции де Гааза- ван Альфена (dHvA)
в серебре Рис.5.2.
Зависимость U(1/B)
Рис.5.2.
Зависимость U(1/B)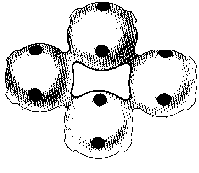 Рис.5.3.
Дырочноподобные траектории электронов
типа "собачьей кости" в благородных
металлах
Рис.5.3.
Дырочноподобные траектории электронов
типа "собачьей кости" в благородных
металлах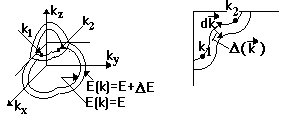 Рис.5.4.
Пояснение к выводу соотношения (5.9)
Рис.5.4.
Пояснение к выводу соотношения (5.9)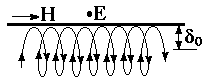 Рис.5.5.
Эффект Азбеля-Канера
Рис.5.5.
Эффект Азбеля-Канера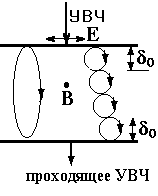 Рис.
5.6. Эффект Гантмахера
Рис.
5.6. Эффект Гантмахера