
- •1.Статистическое описание с позиции классической механики. Функция распределения.
- •Функция распределения.
- •2.Флуктуации аддитивных величин.
- •5. Каноническое распределение в классической статистической теории.
- •6. Термодинамика обратимых процессов.
- •7. Термодинамические функции и термодинамические равенства.
- •8.Классический идеальный одноатомный газ. Распределение Максвелла.
- •9. Классический расчет теплоемкости идеальной кристаллической решетки. Закон Дюлонга и Пти.
- •10. Большое каноническое распределение в классической статистической теории.
- •11.Статистическое описание с позиции квантовой механики.
- •12.Микроканоническое распределение в квантовой статистике.
- •13 И 14.Каноническое и большое каноническое распределения Гиббса в квантовой статистической теории.
- •15 И 16. Квантомеханическое описание колебаний кристаллической решетки. Теплоемкость кристаллической решетки.(при высоких и низких температурах).
- •17. Излучение абсолютно черного тела
- •1Ый Закон излучения Вина
- •2Й закон излучения Вина
- •18.Распределение Ферми-Дирака.
- •19.Идеальный ферми-газ. Плотность одночастичных стационарных состояний. Вычисление термодинамических величин с помощью плотности одночастичных стационарных состояний.
- •21) Вырожденный идеальный электронный газ. Химический потенциал и теплоемкость.
- •22) Электронная теплоемкость металлов.
- •23 И 24.Статистика равновесных носителей заряда в полупроводниках .Электронно-дырочная теплоемкость полупроводников.
- •25.Магнитные свойства вещества. Парамагнетизм газов и электронов проводимости в металлах и полупроводниках
- •Экспериментальные методы исследования поверхности Ферми
- •29. Бозе-Эйнштейна распределение
- •30. Вырожденный идеальный бозе-газ. Конденсация Бозе-Эйнштейна
- •32) Фазовые переходы. Классификация фазовых переходов.
- •33 И 34. Фазовые переходы второго рода. Модель Изинга. Теория Ландау фазовых переходов второго рода.
- •Модель Изинга.
1.Статистическое описание с позиции классической механики. Функция распределения.
Составляя уравнения движения механической системы и интегрируя их, мы принципиально можем получить исчерпывающие сведения об эволюции механической системы. Однако когда мы попытаемся применить методы механики к макроскопической системе, т.е. системе с колоссальным порядка числа Авогадро числом степеней свободы, мы столкнемся с необходимостью составить и решить столь же гигантское число дифференциальных уравнений, что представляется, вообще говоря, невозможным на практике. Следует отметить, что даже если мы получим общее решение уравнений движения такой системы, то совершенно невозможно будет подставить в это решение начальные условия.
Таким образом, нет никакой возможности дать полное механическое описание эволюции состояния макроскопической системы, даже в том случае, когда она замкнута.
Однако, к счастью, для описания подавляющего числа явлений, связанных с макрообъектами, достаточно знать только макроскопические величины, т.е. величины, характеризующие не отдельные частицы, а все тело или его отдельные макроскопические части. Такие величины обладают весьма замечательным свойством.
Из
опыта известно, что если макроскопическое
тело поместить в стационарные условия,
то по истечении некоторого времени
(времени релаксации) оно придет в
состояние термодинамического равновесия.
Это состояние характеризуется тем, что
все макроскопические величины подавляющую
часть времени являются практически
постоянными и лишь сравнительно очень
редко испытывают сколько-нибудь заметные
отклонения. Причем данное обстоятельство
тем более справедливо, чем сложнее и
больше рассматриваемое тело. Указанный
характер поведения макроскопических
величин позволяет при описании таких
систем вместо истинной зависимости
этих величин от времени использовать
их средние по времени значения. Для
величины
 это среднее дается стандартным выражением
это среднее дается стандартным выражением
 .
(1)
.
(1)
Статистическая физика представляет собой математический аппарат, который позволяет вычислять эти средние, не прибегая при этом к указанной формуле. Легко понять что, с помощью этой формулы совершенно нельзя сделать никакие теоретические предсказания значений термодинамических характеристик. Для того, чтобы вычислить среднее с помощью этой формулы, нужно вначале определить зависимость от времени механического состояния системы, т.е. зависимость от времени всех обобщенных координат и скоростей, что невозможно на практике из-за колоссального числа степеней свободы. К счастью оказывается, что как раз наличие у макроскопической системы колоссального числа степеней свободы позволяет вычислять такие средние, не прибегая к этому непосредственному определению.
Прежде, чем перейти непосредственно к обсуждению способов вычисления этих средних, договоримся о некоторой терминологии. Прежде всего, механическое состоянии системы будем называть ее микросостоянием.
Далее
введем понятие фазового пространства
механической системы. Каждое микросостояние
системы с
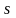 степенями свободы может быть математически
представлено в виде точки в воображаемом
степенями свободы может быть математически
представлено в виде точки в воображаемом
 -мерном
пространстве, по координатным осям
которого откладываются обобщенные
координаты и импульсы. Это воображаемое
-мерное
пространство называется фазовым
пространством системы. Каждая точка
фазового пространства отвечает
определенным значениям координат и
импульсов системы и изображает собой
определенное состояние механической
системы. С течением времени состояние
системы изменяется и соответственно
точка фазового пространства, изображающая
состояние системы, будет описывать в
нем некоторую кривую, которая называется
фазовой траекторией. В дальнейшем, когда
я буду говорить, что система находится
в данной точке фазового пространства,
то я буду иметь ввиду, что система
находится в состоянии, которому отвечает
эта точка фазового пространства. Также
договоримся запись
-мерном
пространстве, по координатным осям
которого откладываются обобщенные
координаты и импульсы. Это воображаемое
-мерное
пространство называется фазовым
пространством системы. Каждая точка
фазового пространства отвечает
определенным значениям координат и
импульсов системы и изображает собой
определенное состояние механической
системы. С течением времени состояние
системы изменяется и соответственно
точка фазового пространства, изображающая
состояние системы, будет описывать в
нем некоторую кривую, которая называется
фазовой траекторией. В дальнейшем, когда
я буду говорить, что система находится
в данной точке фазового пространства,
то я буду иметь ввиду, что система
находится в состоянии, которому отвечает
эта точка фазового пространства. Также
договоримся запись
 обозначать просто
обозначать просто
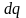 .
Аналогично, запись
.
Аналогично, запись
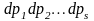 будем обозначать
будем обозначать
 .
Тогда элементарный объем
.
Тогда элементарный объем
 фазового
пространства будет обозначаться
фазового
пространства будет обозначаться
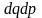 .
.
Приступим теперь к рассмотрению вопроса о том, как можно вычислять статистические средние макроскопических величин, не решая при этом полную механическую задачу
Прежде всего заметим, что макроскопические тела, с которыми нам приходится иметь дело, являются относительно малыми частями большой замкнутой системы, состоящей из внешних тел вместе со средой, в которую они погружены. Например, в случае макроскопического тела, помещенного в термостат, это тело вместе с термостатом образует замкнутую систему. При этом изучаемая нами система очень мала по сравнению с термостатом, так что влияние нашей системы на термодинамическое состояние термостата пренебрежимо мало.
Поэтому постановка нашей задачи должна быть следующей. Рассмотрим замкнутую макроскопическую систему, т.е. систему, не взаимодействующую ни с какими другими телами. Выделим в этой системе некоторую ее часть, которая с одной стороны весьма мала по сравнению со всей системой, а с другой стороны также является макроскопической. Такие относительно малые, но при этом макроскопические части мы будем называть подсистемами. Наша цель состоит в том, чтобы научиться вычислять средние по времени значения макроскопических величин для этих подсистем, не прибегая к решению полной механической задачи. Подсистема сама является макроскопической системой, но при этом уже отнюдь не замкнутой. Напротив, она испытывает всевозможные воздействия со стороны остальных частей системы. Из-за наличия у этих остальных частей системы большого числа степеней свободы эти взаимодействия будут иметь весьма сложный и запутанный характер. Поэтому микросостояние подсистемы будет меняться со временем весьма сложным и запутанным образом. Как раз этот сложный и запутанный характер эволюции микросостояния подсистемы и позволяет подойти к решению поставленной задачи с другой стороны.
В
основе этого подхода лежит то
обстоятельство, что благодаря сложному
и запутанному характеру эволюции
микросостояния нашей подсистемы, она
за достаточно большой промежуток времени
успеет побывать достаточно большое
число раз во всех возможных своих
микросостояниях. Точнее это обстоятельство
можно сформулировать следующим образом.
Выделим достаточно малый объем фазового
пространства
 .
Можно утверждать, что за достаточно
большой промежуток времени
.
Можно утверждать, что за достаточно
большой промежуток времени
 наша подсистема достаточно много раз
пройдет через этот объем фазового
пространства. Пусть
наша подсистема достаточно много раз
пройдет через этот объем фазового
пространства. Пусть
 - часть полного времени
,
в течении которого наша подсистема
находится в точках данного объема
фазового пространства. При неограниченном
увеличении полного времени
отношение
- часть полного времени
,
в течении которого наша подсистема
находится в точках данного объема
фазового пространства. При неограниченном
увеличении полного времени
отношение
 будет стремиться к некоторому конечному
пределу
будет стремиться к некоторому конечному
пределу
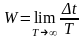 . (2)
. (2)
Этот предел можно, очевидно, рассматривать как вероятность того, что при наблюдении нашей подсистемы в некоторый произвольный момент времени мы обнаружим ее находящейся в данном участке фазового пространства.
