I. Программа курса

1. Линейные пространства

Арифметические векторы и линейные операции над ними.

Если на плоскости ввести систему координат, каждому вектору будет соотв. пара чисел (координат вектора). — вектор а (а1;а2).  ОПР: Арифметическим и n-мерным вектором называется любая последовательность из n чисел (а1 … аn ) или вектор n с его координатами. (а1 … аn ) – координаты вектора. ОПР: Суммой двух векторов называют вектор, координаты которого равны сумме соответствующих координат этих векторов. Свойства: 1. a+b= b+a. 2. (a+ b)+ c= a+ (b+ c). 3. Нулевым вектором будет называться вектор, у которого все координаты – нули: a(0, …, 0)=0, a+ 0= a. 4. Вектор с координатами (-a1, -a2, …, -an) будет называться противоположным вектору а, а+ (-а)= 0. ОПР: Под произведением вектора на число будем подразумевать вектор, координаты которого умножены на данное число. С * вектор а = (са1,са2,…,саn)  СВ-ВА: 1. k(a+ b)= ka+ kb а и b векторы. 2. (k+m)a= ka+ ma a – вектор. 3. k(la)= (kl)a a – вектор. 5. 1a= a, a – вектор.

Векторное пространство .

Определение векторного пространства

Множество   называется векторным пространством, если для него выполняются следующие аксиомы:

V. 1. Множество   является аддитивной абелевой группой.

V.2. Для любого вектора   и любого скаляра – элемента   поля   определено произведение αv, являющееся вектором. Это произведение определено так, что  , где   – единичный элемент поля  .

V.3. Выполняются законы дистрибутивности

и  ,

Где  – скаляры, а   и   – векторы.

V.4. Выполняется закон ассоциативности ,

где      – скаляры, а   – вектор.

 

Свойства векторного пространства

1. Максимальное число линейно независимых векторов в   называется размерностью пространства   над полем  .

2. Совокупность   любых линейно независимых векторов называется базисом n-мерного пространства, если каждый из векторов пространства может быть представлен в виде линейной комбинации этих векторов. Векторы совокупности называются базисными.

3. Подмножество   векторного пространства   такое, что любая линейная комбинация векторов этого подмножества снова принадлежит  , называется подпространством пространства  . Легко проверить, что все векторы подпространства удовлетворяют аксиомам V.1 – V.4. Очевидно, что размерность подпространства не превышает размерности пространства, т.к. во всем пространстве содержится не более   линейно независимых векторов. Каждое подпространство можно рассматривать как самостоятельное пространство. Следовательно, каждое подпространство имеет свой базис.

4. Скалярным произведением двух векторов одинаковой длины  :   и   называется скаляр, определяемый как

.

5. Для векторного пространства определено понятие расстояния между двумя векторами, которое совпадает с нормой разности этих векторов

,

где суммирование производится в поле действительных чисел.

Геометрический смысл пространств 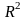и .

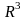ОПР: Множество всех n-мерных арифметических векторов, в которых введены операции: сложение векторов и умножение на число называется арифметическим n-мерным пространством (Rn).

Геометрический смысл имеют лишь пространства R1, R2, R3 . Для R1 – это прямая, для R2 – плоскость, для R3 – трехмерное пространство.

При n>3 пространство Rn представляется лишь чисто математическим и не реальным объектом.

Линейные пространства общего вида.

Множество V называется линейным пространством, а его элементы 0 векторами, если на нем определены 2 операции:

• Сложение векторов, означающее, что каждым двум векторам 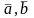по некоторому правилу ставится в соответствие третий вектор, называемый суммой векторов

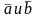
• Умножение вектора на число,

Указанные операции должны удовлетворять следующим условиям (аксиомам):

1) = +

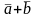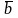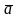
2) ( ) + = + ( + )

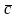3) существует нулевой элемент 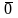, такой, что

+ = для любого

4) для каждого элемента существует противоположный элемент - , такой, что

+(- ) =

5) λ( ) = λ + λ

6) (λ+μ) = λ + μ

7) λ (μ ) = (λμ)

8) 1 * =

Где , и - произвольные элементы V, а λ и μ – произвольные действительные числа, которые принято называть скалярами.

Линейная зависимость системы векторов и ее геометрический смысл.

Система векторов а₁,а₂,…,а_s линейного пространства V называется линейно зависимой, если существуют такие числа с₁,с₂,…,с_s , не равные одновременно нулю, что справедливо равенство с₁а₁ + с₂а₂ + … + с_sa_s = 0

Например, ₁ = (2;2;3), 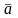₂ = (0;-4;5), ₃ = (3;13;-8) линейно зависимая система векторов, поскольку =(0;0;0)

Свойства линейной зависимости:

1. Система из одного вектора 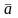линейно зависима тогда и только тогда,когда =

2. Система, содержащая более одного вектора, линейно зависима в том и только в том случае, когда среди данных векторов имеется такой, который линейно выражается через остальные.

3. Если часть система зависима, то и вся система зависима.

4. Если система а₁,а₂,…,а_s линейно независима, но при добавлении к ней еще одного вектора становится зависимой, то вектор линейно выражается через а₁,а₂,…,а_{s .}

Если система векторов а₁,а₂,…,а_s такова, что равенство с₁а₁ + с₂а₂ + … + с_sa_s = 0 возможно, только если с₁=с₂= … =с_s = 0, то эта система называется линейно независимой.

Базис и размерность линейного пространства.

А) Размерность подпространства L( 1 2… s) векторов 1 2… s пространства V называется рангом системы векторов 1 2… s и обозначается rk( 1 2… s). Таким образом, ранг системы равен r, если среди векторов системы существуют r линейно независимых, а любые q>r векторов данной системы линейно зависимы. Ранг же линейно независимой системы равен числу ее членов.

Б)      Базис - любая упорядоченная система   из n линейно независимых векторов пространства  .

Система векторов ₁, ₂, ₃, называется базисом в Rі, если возможны следующие условия:

1. Эти векторы линейно независимы

2. Любой вектор 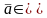Rі является линейной комбинацией векторов данной системы, т.е.

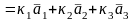
Базис в Rі - это любая упорядоченная система из 3-х линейно независимых 3-мерных векторов.

1. Система линейно независимая, поскольку она линейная.

2. Рассмотрим 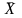=(х₁;х₂;х₃) = (х₁;0;0) + (0;х₂;0) + (0;0;х₃) = х₁(1;0;0) +х₂(0;1;0) + х₃(0;0;1) => - линейная комбинация e₁,e₂ и e₃ => {e₁;e₂;e₃} –базис в Rі.

Если система векторов 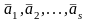такова, что только с₁ā₁+с₂ ā₂+…+с_s ā_s=0 выполняется, только если с₁=с₂=…=с_s, то эта система называется линейно независимой.

Дано: { Ō; ā₁; ā₂;…; ā_n}

Доказать: {Ō; ā₁; ā₂;…;ā} – линейно завис.

Доказательство:

1. {Ō} – л.з. по св-ву 1є линейной зав-ти.

2. (1) c0Ō+Оā1+Оā2+…+Оān = 0 c0 ≠ 0 из (1), значит {Ō; ā1; ā2;…,ān} – линейно зависима по определению, ч.т.д.

Пример: {Ō; ā₁; ā₂}, где ā₁ = (1;1;1), ā₂ = (2;2;2), с₀(0;0;0)+0(1;1;1) + 0(2;2;2) = 0

Координаты вектора в данном базисе

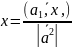
Если система векторов e₁, ..., e_n n-мерного линейного пространства L_n образует базис в L_n, то любой вектор x из L_n может быть представлен в виде

x = С₁·e₁+ С₂·e₂+ ...+ С_n· e_n.

Выражение x = С₁·e₁+ С₂·e₂+ ...+ С_n· e_n называется разложением вектора по базису e₁, ..., e_n, а числа С₁, С₂, ..., С_n называются координатами вектора x  в базисе e₁, ..., e_n.

Координаты вектора принято обозначать тем же символом, что и сам вектор:

x = x₁·e₁+ x₂·e₂+ ...+ x_n· e_n.

Взаимно однозначное соответствие x = x₁·e₁+ x₂·e₂+ ...+ x_n· e_n ⇐⇒ x = (x₁, x₂, ..., x_n)

— изоморфизм L_n и R_n.

Преобразование координат векторов при замене базиса

Пусть системы векторов e = {e₁, ..., e_n} и f = {f₁, ..., f_n} — два базиса n-мерного линейного пространства L_n.

Обозначим x_e = (x₁,x₂, ..., x_n) и x_f = (x'₁,x'₂, ..., x'_n) — координаты вектора x ∈ L_n соответственно в базисах e и f.

Справедливо следующее x_e= C_e→f·x_f :

Здесь C_e→f — матрица перехода от базиса e к базису f, это матрица, столбцами которой являются координаты базисных векторов f₁, ..., f_n  в базисе  e₁, ..., e_n:

f₁ = с₁₁· e₂ + с₂₁· e₁ + ... + с_n1· e_n, f₂ = с₁₂· e₁ + с₂₂· e₂ + ... + с_n2· e_n, ..., f_n = с_1n· e₂ + ... + с_nn· e_n.

Формулу преобразования координат вектора при изменении базиса принято записывать в виде

x_f= (C_e→f)^{− 1}·x_e

Подпространства линейного пространства

Пусть V-линейное пространство, а L-произвольное подмножество (L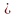 V). Подмножество L называется подпространством линейного пространства V, если оно само является линейным пространством относительно тех же операций сложения и умножения на число, что определены в

Критерии подпространств:

2. для любых двух векторов из L их сумма также принадлежит L

3. для любого вектора из L и любого действительного числа λ произведение λ также принадлежит L

Примеры:

1. Множество всех многочленов, заданных на отрезке [a;b]-подпространством линейного пространства функций, заданных на этом отрезке.

2. Множество всех многочленов, степень которых не превышает n-1, является подпространством множества многочленов, степень которых не превышает n.

3. Множество решений однородной системы линейных уравнений с n неизвестными является подпространством пространства R .

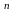dim V≥dim L, где V-линейное пространство, L-его подпростр-во.

Свойства подпространств:

• Подпространство линейного пространства есть линейное пространство

• Размерность подпространства не больше размерности линейного пространства.

• Если e₁, e₂, e₃ – базис подпространства линейного пространства, то

• e_k+1, e_k+2, e_n  R так что, e₁, e₂ e_k  e_n – базис в R.

Скалярное произведение векторов в

Скалярным произведением двух векторов a=(a₁ , a₂ , ..., a_n ) и b=(b₁, b₂, ..., b_n) называется число (a, b)=a₁b₁+a₂b₂+ ...+a_nb_n.

Основные свойства скалярного произведения векторов:

1.( )=( ).

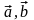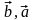2. (k )=k ( )

3. (a+ b, c)=(a, c)+ (b, c)

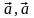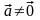4. ( )> 0, если , и если ( )= 0, если

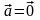
cos.=(a, b)/ |вектор а|*|вектор в|

Равенство справедливо при векторе а0 и векторе в0. Однако формула не совсем проста. Уравнение cos = с, (где  - неизвестное число) имеет решение только при –1c1. Поэтому, чтобы данное нами определение угла между векторами было корректным, необходимо сначала убедиться, что (a, b)/ |вектор а|*|вектор в| заключено между -1 и 1.

Евклидово пространство.

В математике термин евкли́дово простра́нство может обозначать один из двух сходных объектов:

1. Конечномерное вещественное векторное пространство с введённой на нём нормой

где . Также называется конечномерным гильбертовым пространством

2. Метрическое пространство, которое является конечномерным векторным пространством над полем вещественных чисел с метрикой, введённой по формуле:

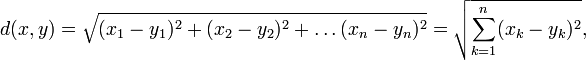
Наглядными примерами евклидовых пространств могут служить пространства размерности n = 1 (вещественная прямая) и размерности n = 2 (комплексная плоскость или евклидова плоскость).

Неравенство Коши-Буняковского.

Для любых двух векторов в евклидовом пространстве справедливо неравенство

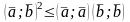
Доказательство:

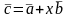, x-произвольное число

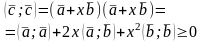
по свойству положительной определенности скалярного произведения

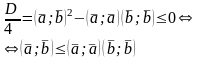
Длины векторов и угол между векторами в

    Длиной (или модулем) n-мерного вектора   называют число  , равное

.

Скалярное произведение   называют скалярным квадратом вектора   и обозначают как  . Квадрат длины вектора   равен его скалярному квадрату, т. е.  .

Если длина вектора равна единице, то вектор называется единичным. Операция приведения вектора к единичной длине называется нормализацией вектора. Среди единичных векторов выделяют векторы, у которых одна координата равна единице, остальные – нулю. Такие единичные векторы называют ортами.

Ортогональный и ортонормированный базисы в .

Координаты вектора в ортогональном базисе.

Процесс ортогонализации.

Ортогональные дополнения подпространств.