
Вопрос 7

Вопрос 8
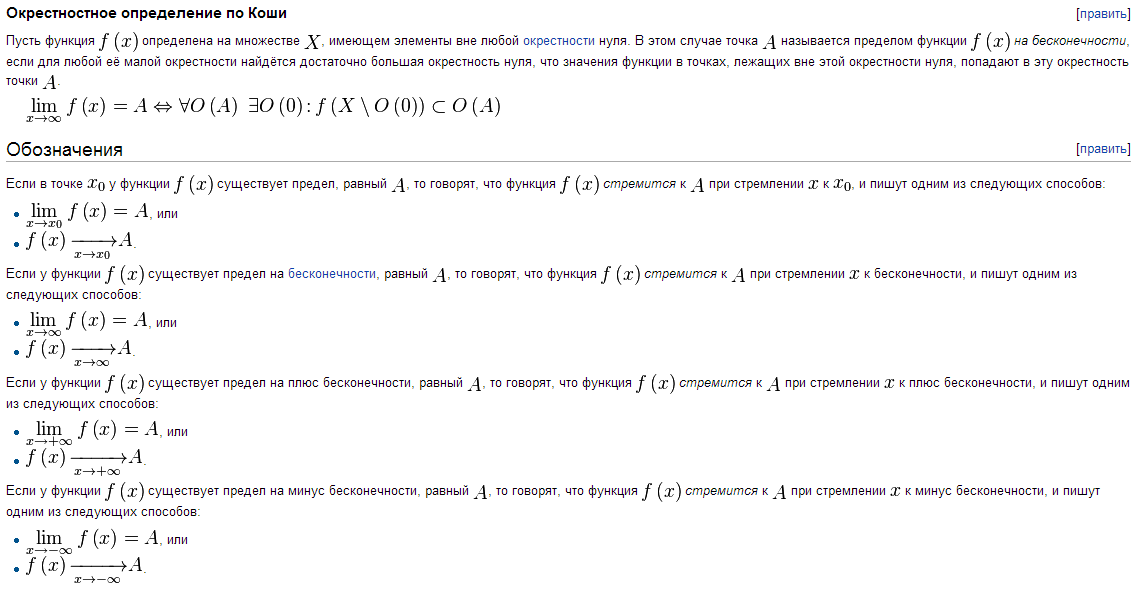
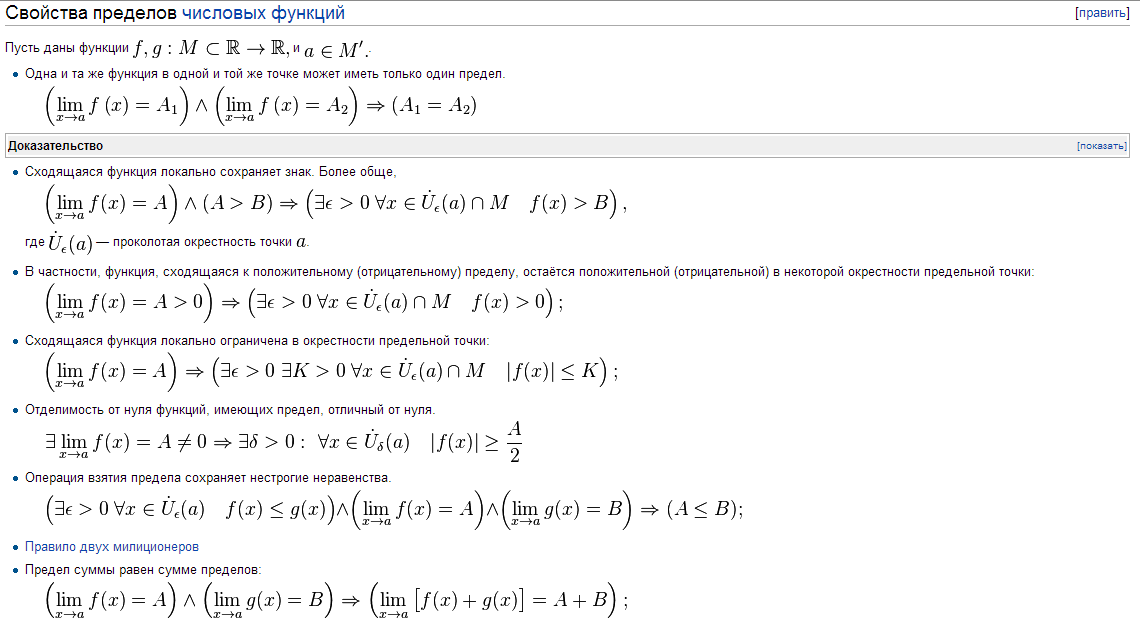
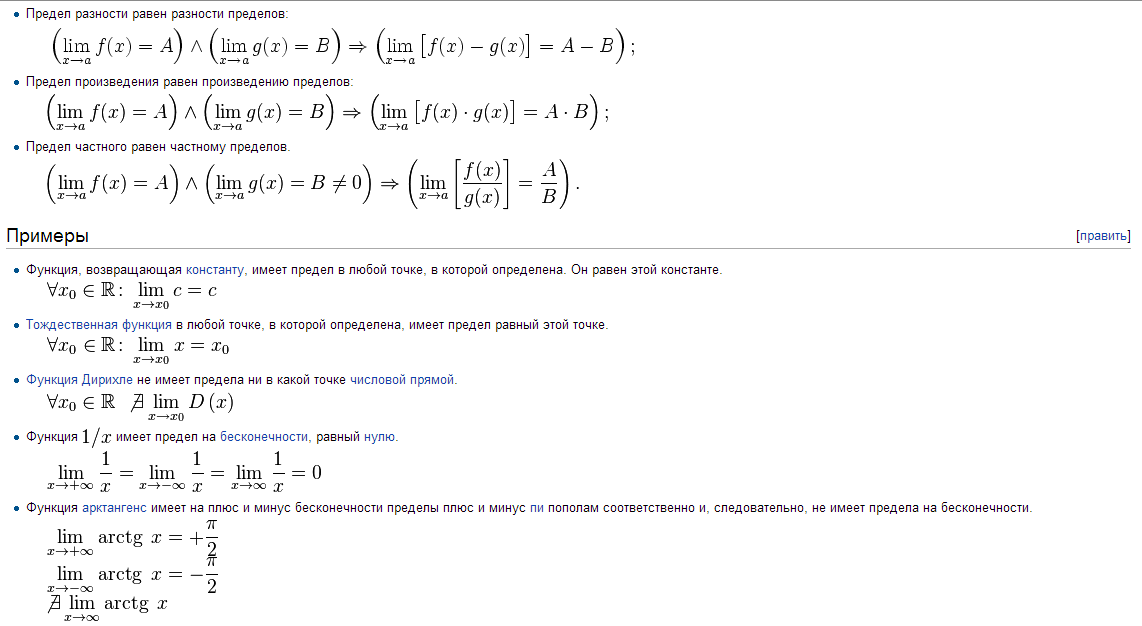
Предел суммы Предел суммы двух функций равен сумме пределов этих функций:
Расширенное правило суммы
Предел постоянной величины Предел постоянной величины равен самой постоянной величине:
Предел произведения функции на постоянную величину Постоянный коэффициент можно выносить за знак предела:
Предел произведения Предел произведения двух функций равен произведению пределов этих функций (при условии, что последние существуют):
Расширенное правило произведения
Предел частного Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
Предел степенной функции
где степень p - действительное число. В частности,
Если f ( x ) = x, то
Предел показательной функции
где основание a > 0. Предел логарифмической функции
где основание a > 0. Теорема "о двух милиционерах" Предположим,
что Точки x = a. Тогда, если
другими функциями, стремящимися к одному и тому же пределу L. |
Пример 1 |
|
Найти
предел Решение. |
Пример 2 |
|
Найти
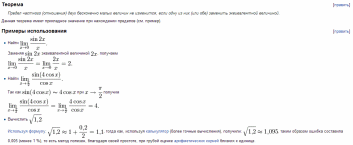
предел Используя основные свойства пределов (правило суммы, правило частного и предел степенной функции), получаем |
Пример 3 |
|
Зная,
что Решение.
|
Пример 4 |
|
Вычислить
предел Решение. Известно,
что Разделив это неравенство на 2x − 7 > 0, получаем (Поскольку мы рассматриваем большие и положительные значения x, и, следовательно, 2x − 7 > 0, то знаки неравенства при делении не изменяются.) Выполняя предельный переход, получаем Вычислим левый и правый пределы: Отсюда, по теореме о "двух милиционерах" следует, что |
Пример 5 |
|
Вычислить
предел Решение. Известно,
что Вычтем 5x из всех частей неравенства. Разделив
на (Знаки
неравенства при этом не меняются,
поскольку
является
положительным числом при Как видно, оба предела равны друг другу. Следовательно, по теореме "o двух милиционерах"
Вопрос 9
Вопрос 10 Непрерывность функции в точке.
Определение. Функция f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точке х0, если предел функции и ее значение в этой точке равны, т.е.
Тот
же факт можно записать иначе:
Определение. Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва.
Пример непрерывной функции:
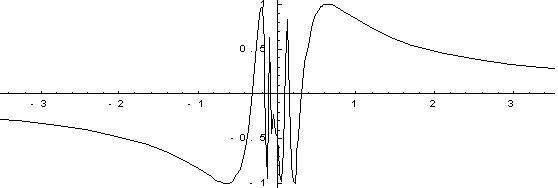
Пример разрывной функции:
Определение. Функция f(x) называется непрерывной в точке х0, если для любого положительного числа >0 существует такое число >0, что для любых х, удовлетворяющих
условию
Определение. Функция f(x) называется непрерывной в точке х = х0, если приращение функции в точке х0 является бесконечно малой величиной.
f(x) = f(x0) + (x) где (х) – бесконечно малая при хх0.
Свойства непрерывных функций.
непрерывная в точке х0.
что g(x) не равна нулю в точке х0.
3) Суперпозиция непрерывных функций – есть непрерывная функция. Это свойство может быть записано следующим образом: Если u = f(x), v = g(x) – непрерывные функции в точке х = х0, то функция v = g(f(x)) – тоже непрерывнаяфункция в этой точке.
Справедливость приведенных выше свойств можно легко доказать, используя теоремы о пределах.
Непрерывность некоторых элементарных функций.
1) Функция f(x) = C, C = const – непрерывная функция на всей области определения.
кроме тех, при которых знаменатель обращается в ноль. Таким образом, функция этого вида непрерывна на всей области определения.
3) Тригонометрические функции непрерывны на своей области определения. Докажем свойство 3 для функции y = sinx. Запишем приращение функции y = sin(x + x) – sinx, или после преобразования:
Действительно,
имеется предел произведения двух
функций
этом
функция косинус – ограниченная функция
при х0
предел
функции синус Таким образом, имеется произведение ограниченной функции на бесконечно малую, следовательно это произведение, т.е. функция у – бесконечно малая. В соответствии с рассмотренными выше определениями, функция у = sinx – непрерывная функция для любого значения х = х0 из области определения, т.к. ее приращение в этой точке – бесконечно малая величина.
Вопрос 11
Вопрос 12 Сравнение бесконечно малых функций Пусть α(x) и β(x) две бесконечно малые функции при x → x0 и β(x) отлична от нуля в некоторой окрестности
точки х0 (за исключением, быть
может, самой точких0). Если
то α(x) называется бесконечно малой более высокого порядка, чем β(x) . В этом случае пишут α(x) = o(β(x)) и говорят α(x) есть о − малое от β(x). Если = А ≠ 0 ( A - число), то бесконечно малые α(x) и β(x) имеют одинаковый поряок малости. В этом случае пишут α(x) = O(β(x)), (α(x) есть O - большое от β(x). Если = ∞, то α(x) называется бесконечно малой более низкого порядка, чем β(x). Если = 1, то α(x) и β(x) называется эквивалентными бесконечно малыми, α(x) ~ β(x). В некоторых случаях недостаточно знать, что одна из двух бесконечно малых является бесконечно малой более высокого порядка, чем другая. Нужно еще оценить, как высок этот порядок. Поэтому вводится следующее правило: если
то α(x) является бесконечно малой n -го порядка относительно β(x). Теорема. Для того, чтобы две функции f = f (x) и g = g (x), f (x) ≠ 0, g (x) ≠ 0, были эквивалентными при х → х0, необходимо и достаточно, чтобы выполнялось хотя бы одно из условий f - g = o(f ) или f - g = o(g). Доказательство необходимости. Пусть
Аналогично
из условия
Вопрос 13
|

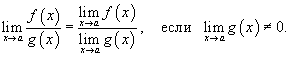
 .
Решение.
.
Решение.

 .
.
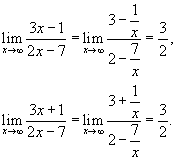
 .
.




 .
.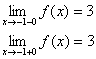 непрерывна
для всех значений х,
непрерывна
для всех значений х,



 =
0,
=
0, ,
, ,
тогда
,
тогда
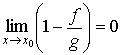 ,
откуда
,
откуда
 ,
то есть g − f = o(g).
,
то есть g − f = o(g).
 доказывается g − f = o(f )
доказывается g − f = o(f )