Вопрос 2

В математике пределом последовательности называют объект, к которому члены последовательности в некотором смысле стремятся или приближаются с ростом номера. Предел — одно из основных понятий математического анализа. Понятие предела использовалось ещё Ньютоном во второй половине XVII века и математиками XVIII века, такими как Эйлер и Лагранж, однако они понимали предел интуитивно. Первые строгие определения предела последовательности дали Больцано в 1816 году и Коши в 1821 году. Не у всякой последовательности существует предел. Например, если взять в качестве пространства множество вещественных чисел со стандартной топологией, а в качестве последовательность , то у неё не будет предела. Если у последовательности существует предел, то она называется сходящейся, если нет — расходящейся. В общем случае пределов может быть несколько. Например, если пространство снабжено антидискретной топологией, то пределом любой последовательности будет любой элемент пространства. Однако при наложении некоторых условий на пространство можно достичь единственности предела в случае его существования.

Случай вещественных чисел

Пределом последовательности вещественных чисел называется число , если выполнено следующее условие:

то есть для любой окрестности точки можно указать номер, начиная с которого все элементы последовательности будут лежать в этой окрестности. Также можно дать эквивалентное определение: число называется пределом последовательности, если в любой его окрестности содержится бесконечное число элементов последовательности, а вне этой окрестности — лишь конечное число. Таким образом, пределом последовательности может быть только предельная точка множества её элементов. Это определение согласуется с общим определением предела для топологических пространств.

Если последовательность имеет предел, то она называется сходящейся к числу , если нет, торасходящейся. Тот факт, что число является пределом последовательности , записывается следующим образом: . Это определение обладает неустранимым недостатком: оно объясняет, что такое предел, но не даёт ни способа его вычисления, ни информации о его существовании. Всё это выводится из доказываемых ниже свойств предела. Всё вышесказанное относилось к конечным пределам, но определение предела можно расширить и на бесконечные значения: и . Для примера запишем определение предела, равного плюс бесконечности: . Термин «сходящаяся последовательность» не распространяется на последовательности с бесконечными пределами.

Свойства

Имеют место следующие арифметические свойства пределов вещественных последовательностей:

, где — константа;

, если указанные пределы существуют;

при том же условии;

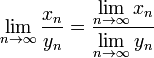, если пределы существуют и .

Свойства 1—3 очевидным образом выводятся из определения предела; докажем последнее свойство. Для начала нужно доказать, что сходится к , где — предел .