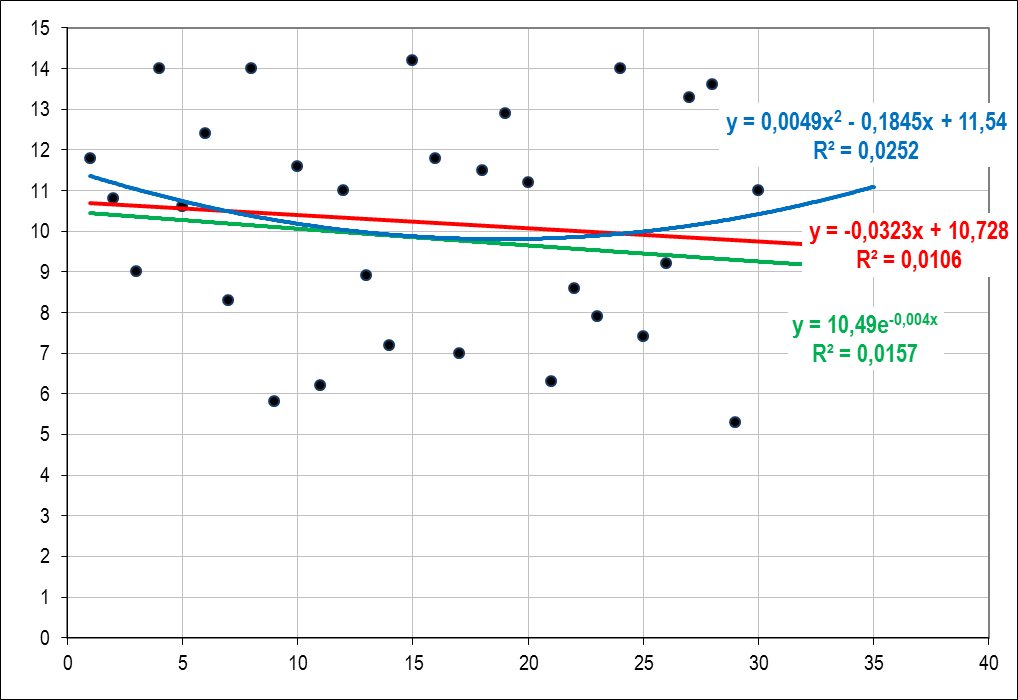
Пример необоснованного применения линейного тренда для описания данных.

Коэффициент детерминированности R² близок к 0.

Нерегулярная компонента. Анализ остатков

Основной критерий качественной модели прогноза – остатки прогноза ε_i = Y_i - F(t_i), т.е. разности между значениями функции прогноза F(t_i) и соответствующими значениями временного ряда Y_i являются случайными числами с функцией распределения, близкой к нормальному распределению.

Общая идея: если это не так, то какая-то закономерность в ряду данных не описана использованной моделью прогноза, либо модель вообще не верна.

Несколько критериев для проверки ряда остатков.

1. Остатки случайны при оценке их временной диаграммы «на глаз».

Отсутствует тренд или какой-нибудь другой «рисунок» на диаграмме остатков.

И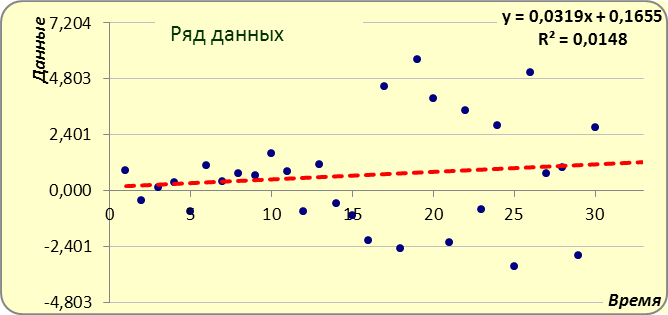 х стандартное отклонение s постоянно и не зависит от t_i (гомоскедастичность).

Любая, видимая на глаз, упорядоченность в диаграмме остатков свидетельствует либо о не полной случайности остатков прогноза, либо о несоответствии их нормальному распределению.

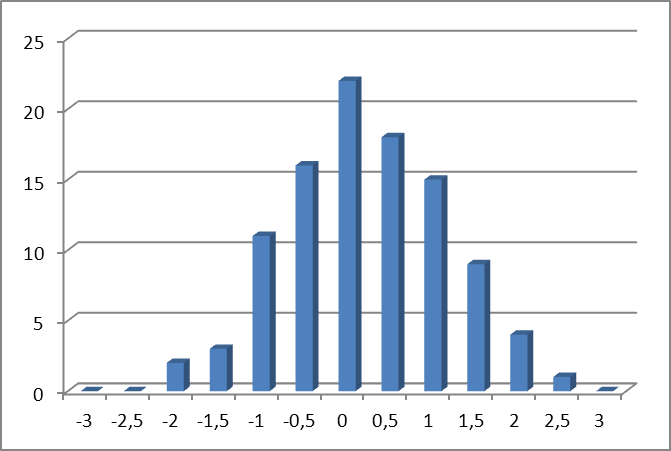
2. Гистограмма остатков прогноза соответствует нормальному распределению (при достаточной статистике).

3. О 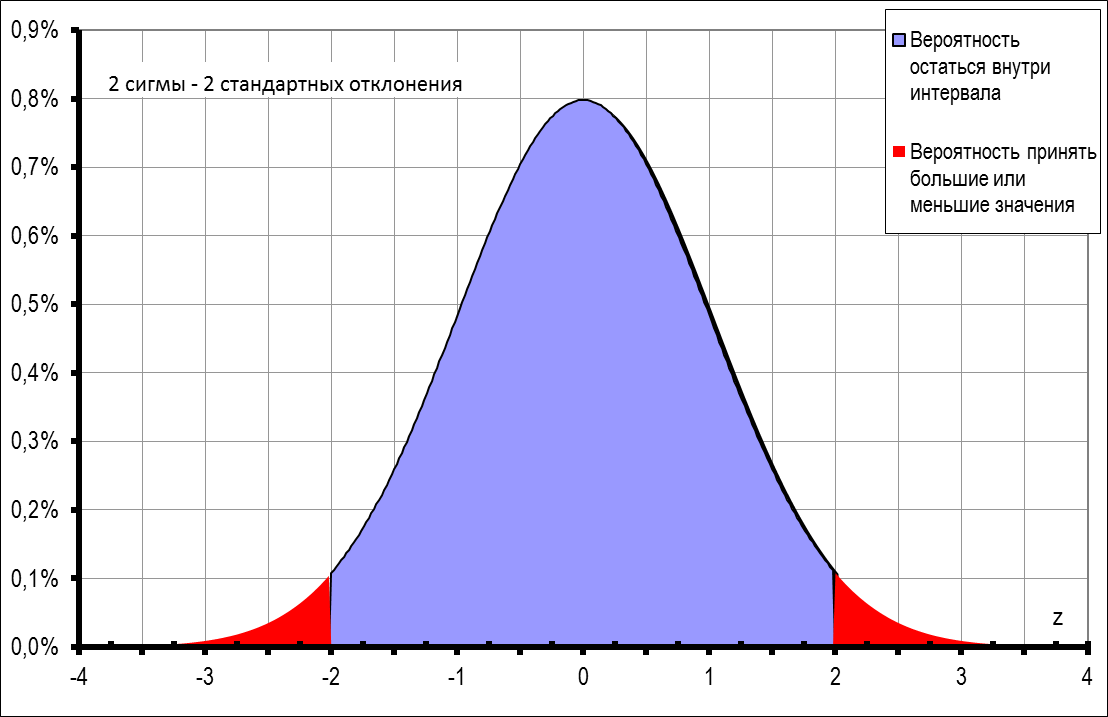коло 95% точек на диаграмме остатков лежат в интервале 2s (стандартных отклонения).

4. Среднее значение ряда остатков близко к нулю, точнее (s- стандартное отклонение, N – полное количество точек временного ряда).

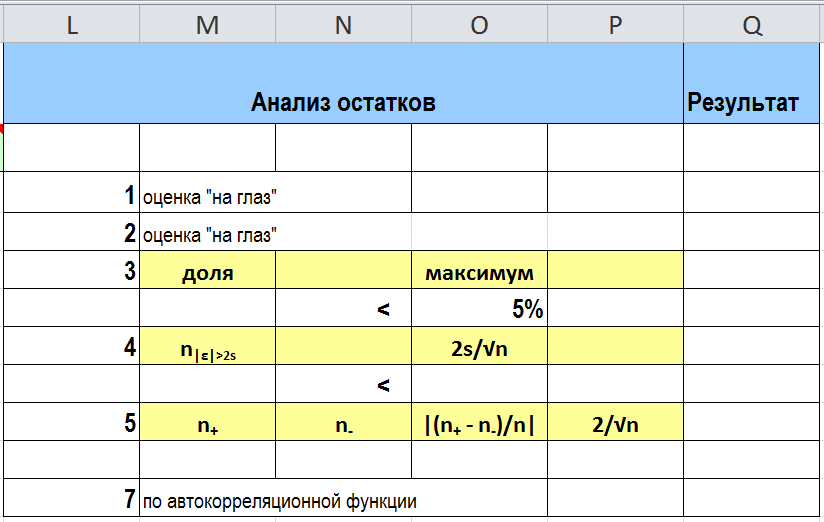
5. Количество положительных и отрицательных остатков примерно одинаково, точнее разность между долями положительных и отрицательных остатков не выходит за пределы интервала:

6. Остатки независимы друг от друга, не коррелированы, точнее сказать, значения автокорреляционной функции r ^ac_m лежат в пределах  2/N.

Здесь ε_i – ряд остатков, m – лаг (интервал), для которого считается корреляция, s – стандартное отклонение ряда остатков. Средние значения ε_[1…N-m] и ε_[m+1…N] — средние значения рядов, полученных из исходного отбрасыванием m чисел в конце и в начале соответственно (при большой статистике практически равны друг другу).

Прим. Более аккуратно предельный уровень случайных корреляций оценивается по формуле ±t*se(r_m), где при значимости 95% по распределению Стьюдента t =СТЬЮДРАСПОБР(0,05; df) или t =СТЬЮДЕНТ.ОБР.2Х(0,05; df) (в Excel 2010), df – число степеней свободы (N-1), а ошибки оценки se равны:

Для числа точек больше 30 величину t обычно принимают равной 2, для меньшего числа точек t вычисляют, так как она увеличивается (при df=10 → t =2.23).

Анализ остатков

Заполните следующую таблицу результатов анализа остатков по 6 критериям.

О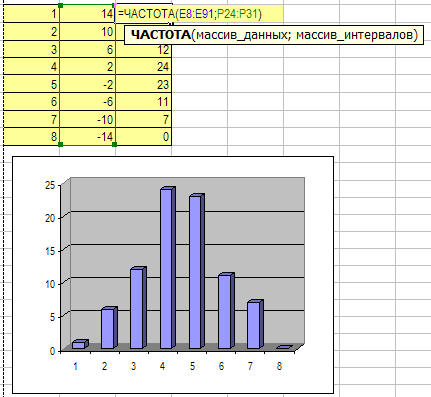 ценка «нормальности» распределения по частотной диаграмме.

6. Для проведения анализа воспользуемся инструментом ACF - автокорреляционная функция. Для этого нужно подключить специальную надстройку Acf.xla. (Меню Сервис\Надстройки -> отметить Acf или просто запустить файл Acf.xla, разрешив запуск макросов).

Откройте меню Сервис, найдите пункт Автокорреляционная функция, щелкните левой кнопкой мыши. В появившемся меню

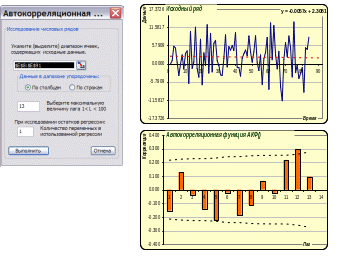
укажите диапазон остатков прогноза (E8:E91) и максимальную величину лага, которую следует проверить.

Так как приведены годичные данные имеет смысл проверить корреляции членов ряда, отстоящих друг от друга на 12-13 месяцев.

После того, как будет нажата кнопка «Выполнить», в книге Excel добавится новый лист с двумя диаграммами.

На верхней диаграмме - исходный временной ряд с линией тренда для оценки остаточного тренда. Цена деления оси данных - стандартное отклонение остатков, так что диаграмма может использоваться для оценки числа точек, выходящих за границы 2s.

На нижней диаграмме - собственно автокорреляционная функция. Пунктиром показан порог "белого шума", превышение которого свидетельствует о наличии корреляций указанного порядка.

Используйте полученные данные для заполнения таблицы анализа остатков.