Построение линии тренда для произвольной функции.

Следующий принципиально важный набор данных возьмем со страницы «ЛогТ» файла «01_Аппроксимация.xls».

Построим как обычно график – точечную диаграмму.

Здесь хорошо видно, что точки не лежат на одной прямой, так что линейный тренд не подойдет. Тем не менее, добавим линию тренда и попробуем подобрать наилучшую.

Есть ли какая-то линия тренда, подходящая для описания этого набора данных?

Попробуйте использовать различные линии тренда для аппроксимации этих данных.

Что делать, если ни одна линия тренда из стандартного набора MS Excel не подходит?

Если у вас есть идея о том, какая бы математическая функция могла подойти, можно сделать то же самое, что делает Excel для подбора линии тренда. Делает..., но не показывает пользователю.

Для самостоятельного подбора наилучших параметров произвольной функции в качестве линии тренда нужно выполнить пять действий:

1. Записать уравнение функции в общем виде, т.е. заменив параметры функции латинскими, к примеру, буквами.

2. Выделить на листе Excel ячейки под каждый из параметров функции.

3. Рядом со столбцом исходных данных рассчитать столбец линии тренда, соответствующей выбранной функции. Для этого в каждую ячейку столбца линии тренда нужно поместить функцию тренда, сославшись на ячейки с параметрами функции и на ячейку независимой переменной.

4. Добавить на график с данными график с числами из столбца линии тренда.

5. Подобрать параметры функции так, чтобы линия тренда как можно лучше соответствовала данным.

Наиболее трудной частью здесь оказывается выбор вида функции. Во многих случаях это может вылиться в серьезную исследовательскую работу.

Но сейчас мы просто примем к сведению, что похожий вид имеет логиста – логистическая функция:

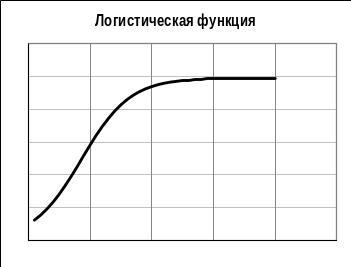
Логиста сначала быстро растет, но потом замедляется и постепенно приближается к горизонтальной асимптоте.

Формулу для этой функции записывают по-разному, а наиболее ясная, на взгляд автора, форма такая:

F = N / ((N/N₀-1) * exp( -α * t) + 1)

Видно, что в этой функции три параметра: N, N₀ и α. 

Эти параметры имеют достаточно прозрачный геометрический смысл. N₀ – значение функции в самом начале (слева). N – максимальное значение функции, т.е. значение функции на «плато» справа. α – параметр, задающий скорость роста кривой в средней части. Значения параметра не выходят за границы 0...1.

Если данные временного ряда точно ложатся на какую-либо математическую кривую и могут быть точно описаны математической функцией – параметры этой функции можно точно подобрать с помощью метода наименьших квадратов.

Метод наименьших квадратов

MSE (Mean Squared Error) — среднеквадратичная ошибка прогноза;

Следует выбрать вид и параметры функции f(t) так, чтобы величина mse была минимальной.

Метод наименьших квадратов (Least-squares method)

Основной метод построения прогноза. Параметры кривой прогноза, сглаживающей изменения экономического показателя, должны быть подобраны так, чтобы сумма квадратов отклонений реальных данных от линии прогноза была минимальной.

R² — коэффициент детерминированности или величина достоверности аппроксимации;

Полная сумма квадратов отклонений (от среднего):

Сумма квадратов отклонений от линии прогноза:

Формула для логистической кривой F = N / ((N/N₀-1) * exp( -α * t) + 1)

Параметры функции N, N₀ и α заданы «на глаз», только чтобы получить видимую на диаграмме линию.

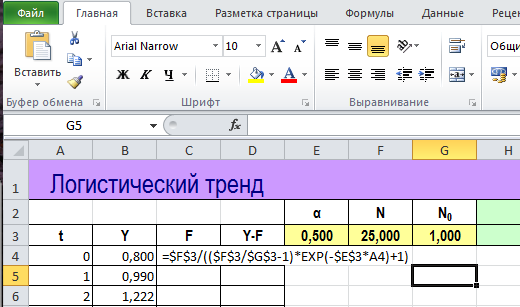
Попробуйте подобрать параметры тренда N, N₀ и α так, чтобы он лучше соответствовал данным.

Чтобы автоматизировать поиск наилучших параметров по методу наилучших квадратов нужно вычислить разности между исходными данными (столбец B) и точками тренда (столбец С).

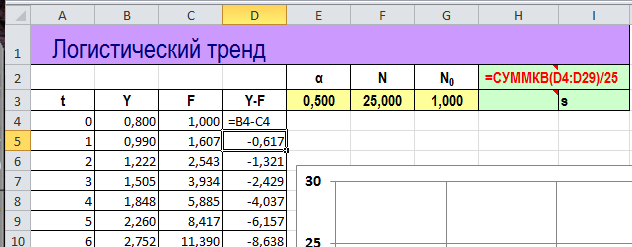
А затем сумму квадратов отклонений (ячейка H2).