
- •Глава 2 антенны
- •2.1. Основные параметры антенных устройств
- •2.2. Элементарные источники излучения
- •2.3. Теорема перемножения диаграмм направленности
- •2.4. Линейная периодическая система излучателей
- •2.5. Плоская синфазная система излучателей
- •2.6. Непрерывное распределение токов на излучающем элементе
- •2.3. Линейные электрические вибраторы
- •2.4. Рупорные антенны
2.4. Рупорные антенны
Рупорные антенны по существу представляют собой открытый конец волновода равномерно расширяющийся в одной или двух плоскостях (Е и Н). Поэтому целесообразно, сначала рассмотреть излучение открытого конца волновода с волной Н10. Распространяющаяся по волноводу волна, дойдя до открытого конца, частично отражается обратно, а частично излучается. Строгого решения данной задачи для прямоугольного волновода до настоящего времени не найдено. Недостатком излучателя в виде открытого конца волновода является значительный коэффициент отражения от конца волновода. Для этого используют согласующие устройства в виде рупора.
Излучение открытого конца прямоугольного волновода.
Электромагнитное поле в сечении открытого конца волновода (раскрыве) прямоугольного волновода можно считать таким же, как в произвольном сечении волновода с волной H10, т.е.

Определим поле в дальней зоне, считая, что в раскрыве волновода размером а×b с волновым сопротивлением WH, размещены одинаково ориентированные излучатели Гюйгенса, (рис. 2.15). При этом волновое сопротивление свободного пространства равно W0.
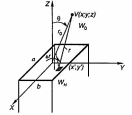
Рис. 2.15
Интегрируя
по раскрыву волновода, получим
электрическую составляющую поля в
главных плоскостях (в плоскостях
XOZ
— плоскость
вектора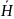 ,
YOZ
— плоскость
вектора
,
YOZ
— плоскость
вектора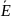 в
волноводе
соответственно):
в
волноводе
соответственно):
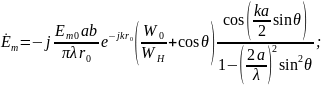
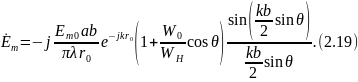
Используя
соотношение, (2.3) определим КНД открытого
конца волновода. Так как из (2.19) следует,
что амплитуда максимальной напряженности
поля равна
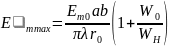 ,
а максимальная мощность, передаваемая
по волноводу равна
,
а максимальная мощность, передаваемая
по волноводу равна
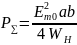 ,
с учетом (2.3) находим:
,
с учетом (2.3) находим:
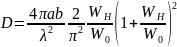
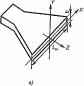
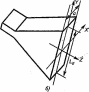
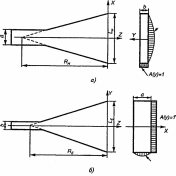
Излучение рупорных антенн. Для увеличения направленности и уменьшения отражения от открытого конца волновода используют рупорные антенны, к основным типам которых относятся: секториальные, пирамидальные и конические рупоры. Секториальным называют рупор, у которого увеличивается один из размер поперечного сечения прямоугольного волновода, а второй остается неизменным, при увеличении размера волновода в плоскости Н называют H-секториальным рупором (рис. 2.16, а), при увеличении размера в плоскости Е называют называют E-секториальным (рис. 2.16, б).
Пирамидальный рупор, у которого увеличены размеры в двух плоскостях: Е и Н. Конический рупор выполнен на основе круглого волновода, его раскрыв может быть круглым, эллиптическим или какого-либо другого вида.
Для определения диаграммы направленности рупорной антенны
будем считать, что токи не затекают на внешнюю поверхность рупора, а поле в раскрыве рупора можно считать равным полю падающей волны в соответствующем сечении этого рупора при бесконечной его длине. При этом волны высших типов, возникающие вблизи раскрыва, не учитываем, также не учитываем наличие отражений при достаточно длинном рупоре WH → W0. С учетом данных приближений можно с достаточной степенью точности определить поле диаграммы направленности в области главного лепестка и нескольких первых боковых лепестков.
 Д
Д
Рис. 2.16
ля определения структуры поля надо знать амплитудно-фазовое распределение в раскрыве рупора. Определим его.Анализ показывает, что в Н- и Е- секториальных рупорах в дальней зоне устанавливается волна цилиндрического типа. Учитывая особенности распространения такой волны для H-векториального рупора, можно получить следующее соотношение для амплитудно-фазового распределения поля в раскрыве:
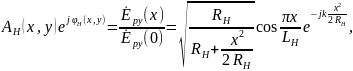
где RH и LH соответственно длина и размер рупора в плоскости ; индекс «р» показьшает, что данное поле создается рупором (рис. 2.17, а).
Так как на практике обычно RH > LH, то
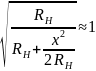
и
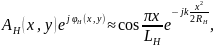
 т.
е. амплитудное распределение в раскрыве
рупора в H-плоскости
такое же, как в питающем его прямоугольном
волноводе, а фаза изменяется по
квадратичному закону.
т.
е. амплитудное распределение в раскрыве
рупора в H-плоскости
такое же, как в питающем его прямоугольном
волноводе, а фаза изменяется по
квадратичному закону.
Рис. 2.17
Аналогично для Е-секториального рупора получим следующее амплитудно-фазовое распределение в раскрыве:
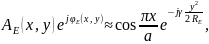
где
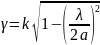 —
фазовая скорость волны в питающем
волноводе; RE
и LЕ
— длина и размер раскрыва рупора
соответственно (рис. 2.17, б).
—
фазовая скорость волны в питающем
волноводе; RE
и LЕ
— длина и размер раскрыва рупора
соответственно (рис. 2.17, б).
Амплитудное распределение в раскрыве рупора в плоскости Е равномерное, а фаза изменяется по квадратичному закону. В плоскости H амплитудное распределение косинусоидальное как в прямоугольном волноводе.
Распределение амплитуды и фазы в раскрыве пирамидального рупора (как при RE = RH, так и при RE ≠ RH) определяется соотношениями:
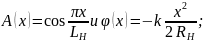
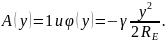
Амплитудно-фазовые распределения в раскрывах рупоров, полученные выше, позволяют определить создаваемые ими диаграммы направленности.
В Е-
и H-плоскостях,
получаются такие же диаграммы
направленности, как и для линейных
систем с равномерным (E-плоскость)
и косинусоидальным (H-плоскость)
амплитудными распределениями и
квадратичными фазовыми распределениями.
При малых фазовых искажениях (в
E-плоскости
меньше
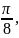 в H-плоскости
меньше
в H-плоскости
меньше
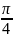 )
можно считать
раскрывы рупоров синфазными с амплитудным
распределением
)
можно считать
раскрывы рупоров синфазными с амплитудным
распределением
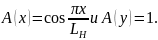
Соотношения для расчета полей вEиHплоскостях, аналогичны выражениям для открытого конца прямоугольного волновода (2.19), в которых необходимо заменить значение а на LH, b на LE и WH на W0. При этом нормированные диаграммы направленности определяются соотношениями:
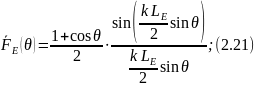
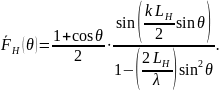
Определить ширину диаграммы направленности в главных плоскостях (в градусах) можно по следующим формулам:
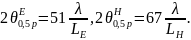
КНД рупорных
антенн можно определить по формуле
(2.3) или воспользоваться рассчитанными
графиками, на которых представлены
зависимости КНД H-
и E-секториальных
рупоров в функции от размеров раскрыва
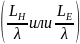 при различных значениях относительной
длины рупора
при различных значениях относительной
длины рупора
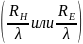 — рис. 2.18. На приведенных графиках КНД
соответственно
DH
и DE
размер «b»
— для H-рупора
и «а»
— для E-рупора
взят равным длине волны λ,
для которой определяются параметры
рупора. Для рупоров, у которых этот
размер не равен λ,
полученные значения DH
и DE
следует
умножить соответственно на
— рис. 2.18. На приведенных графиках КНД
соответственно
DH
и DE
размер «b»
— для H-рупора
и «а»
— для E-рупора
взят равным длине волны λ,
для которой определяются параметры
рупора. Для рупоров, у которых этот
размер не равен λ,
полученные значения DH
и DE
следует
умножить соответственно на
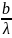 или
или
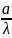 .
.
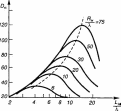
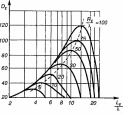
Максимум значений
DH
и DE
(рис.
2.18) обусловлен тем, что увеличение
размера раскрыва рупора
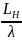 или
или
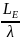 без увеличения
без увеличения или
или
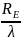 приводит
к росту фазовых искажений на краю рупора
и, следовательно, к падению КНД. А
увеличение длины рупора при постоянной
величине раскрыва приводит к увеличению
затекания токов на внешнюю сторону
рупора и увеличению уровня боковых
лепестков. Это также приводит к снижению
КНД. Поэтому есть оптимальные значения
размеров Н
приводит
к росту фазовых искажений на краю рупора
и, следовательно, к падению КНД. А
увеличение длины рупора при постоянной
величине раскрыва приводит к увеличению
затекания токов на внешнюю сторону
рупора и увеличению уровня боковых
лепестков. Это также приводит к снижению
КНД. Поэтому есть оптимальные значения
размеров Н
Рис. 2.18
- и E-секториальных рупоров. Оптимальным размерам рупоров, обладающих максимальным значением КНД, соответствует пунктирная кривая графиков, показанная на рис. 2.18. Оптимальному рупору соответствует величина фазовой ошибки на его краю раскрыва равная для H-рупора
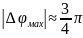 ,
а для E-рупора
,
а для E-рупора
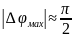 .
Из этих условий определены размеры
длины R
оптимального рупора в зависимости от
величины LH
и LE
раскрыва:
.
Из этих условий определены размеры
длины R
оптимального рупора в зависимости от
величины LH
и LE
раскрыва:
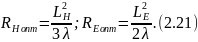
При этом коэффициент использования поверхности оптимальных рупоров vопт = 0,64, а ширина диаграммы направленности для оптимальных рупоров равна:
для H-рупора
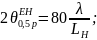
для E-рупора
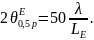
Для пирамидального рупора КНД находится по формуле:
D=0,1DHDE.
Значение DH и DE берутся из графиков рис. 2.18.
При известных значениях RH и RE пирамидального рупора его КНД определяется соотношением:
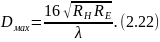
В оптимальном
пирамидальном рупоре фазовые искажения
на краях раскрыва в E-плоскости
равны
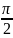 и в Н-плоскости
-
и в Н-плоскости
-
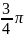 .
При этом коэффициент использования
поверхности такого рупора составляет
величину vпир=0,5.
.
При этом коэффициент использования
поверхности такого рупора составляет
величину vпир=0,5.
Для формирования более узких диаграмм направленности с помощью рупоров используют фазокорректирующие устройства (линзы из диэлектрика, металлопластинчатые линзы и т.п.).
Рупорные антенны используются, как в качестве самостоятельных антенн, так и в качестве облучателей зеркальных антенн.
