2.3. Теорема перемножения диаграмм направленности

Поле для системы N излуча­телей в дальней зоне в некоторой точке М(θ, α) равно сумме полей от всех излучателей

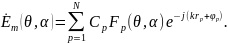
Здесь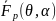 — диаграмма направленности р-го излучателя систе­мы; С_р — множитель, определяющий интенсивность колебаний для этого излучателя; r_р и φ_р — соответственно расстояния р-го излуча­теля до точки наблюдения и фазы его тока возбуждения; k — волновое число, k = (2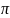 )/λ.

Если все излучатели имеют одинаковые диаграммы направленности и одинаково ориентированы, т. е.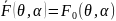 , то

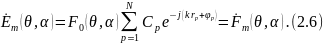
где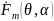 — ненормированная комплексная диаграмма направ­ленности данной системы излучателей по полю.

Из соотношения (2.6) следует теорема перемножения диаграмм, играющая в теории антенн большую роль. Диаграмма направленности системы однотипных оди­наково ориентированных излучателей есть произведение диаграм­мы направленности одного из излучателей на множи­тель комбинирования (или называемый также множителем системы).

Множитель комбинирования (диаграмма направленности) характеризует результат сложения системы излучателей при замене каждого из них на изотропный (точечный) источник излучения.

Нормированная диаграмма направленности си­стемы излучателей имеет следующий вид:

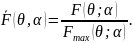
2.4. Линейная периодическая система излучателей

Найдем поле в точке М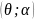 дальней зоны от линей­ной периодической системы однотипных изотропных излучателей, расстояние между которыми d, а разность фаз Δφ, размещенной вдоль оси X систе­мы координат X, Y, Z.

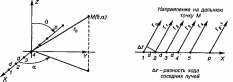
Поле равно сумме полей от всех излучателей (рис. 2.4). Принимая во внимание, что r λ и r d, разность хода до точки М для соседних излучателей равна r_p = d cos α sin θ, а разность хода для р-го излучателя r_p = r₀ – (p–1) Δr, а его фаза φ_р = Δφ – (р – 1). Так как по условию С_р = С₀, поле в точке М для системы N излучателей равно

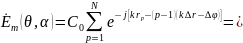
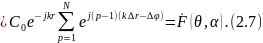
Полученное выражение характеризует комплексную диаграмму направлен­ности системы по полю. Вычисляя сумму в (2.7), как сумму геомет­рической прогрессии и учитывая лишь амплитуду в полученном выражении, получим выражение для ненормированной диаграммы направленности по полю:

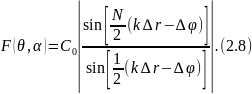
Значение Δr называют «разностью хода лучей» двух соседних излучателей.

Рис. 2.4

Если излучатели расположены вдоль оси X, то Δr = Δr_x = d cosα sinθ; если вдоль оси Y, то Δr = Δr_y = d sin α sin θ; если вдоль оси Z, то Δr = Δr_z = d cos θ.

Нормированная диаграмма направленности имеет вид

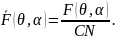
Если излучатели системы являются не изотропными, а направленными, определяемыми нормированной диаграммой F₀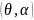 , то в соответ­ствии с теоремой перемножения диаграмм общая диаграмма напра­вленности равна

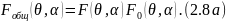
Выражение (2.8) позволяет рассмотреть антенные си­стем из син-фазных дискретных излучателей (∆φ = 0) и со сдвигом фазы ∆φ ≠ 0.

Для системы из синфазных излучателей максимум излучения ориентирован перпендикулярно оси размещения излучателей. В этом случае параметры диаграммы направленности (ширину по уровню мощности 0,5, по первому нулю, место­положение нулей и максимумов боковых лепестков) можно опреде­лить из анализа соотношения (2.8) при ∆φ = 0.

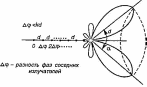
При сдвиге фаз ∆φ ≠ 0 имеем антенну бегущей вол­ны, для которой диаграмма направленности наклонена к оси размещения излучателей на угол α, который опреде­ляется следующим соотношением

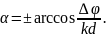
Д

Рис. 2.5

анное соотношение имеет смысл при ∆φ ≤ kd. При kd > ∆φ угол α действительный, а диа­грамма направленности представляет собой неко­торое тело вращения вокруг оси излучателей (рис. 2.5). При увеличении отношения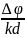 угол α умень­шается, а при ∆φ = kd α = 0 и максимум излучения направлен по оси системы излучателей (осевое излучение).

Из (2.8) можно определить условия, при которых осевая диаграмма не будет иметь обратного излучения:

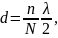
где п = 1, 2, 3..., а N — число излучателей; при этом отношение n/N должно быть нецелым числом.

Э

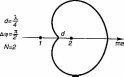
Рис. 22.62.62.6

ти условия позволяют определить параметры простейшей ан­тенны бегущей волны, состоящей из двух дискретных излучателей: при этом N=2, а n = 1, так как n/N должно быть нечетным и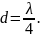 Диаграмма направленности системы — однонаправленная и имеет вид кардиойды (рис. 2.6).