54. Основні залежності між індексами.

Деякі індекси пов’язані між собою такими важливими співвідношен­нями:

1. Добуток індивідуальних ланцюгових індексів дорівнює кінцевому базисному. Наприклад,

.

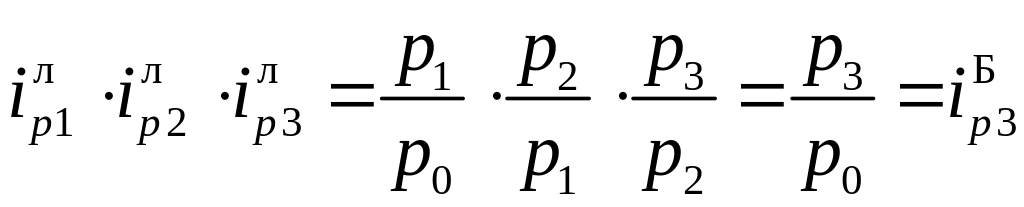У багатьох випадках ця ж залежність справедлива і для загальних індексів.

2. Якщо деякий показник дорівнює добутку інших показників, то його індивідуальний індекс дорівнює добутку відповідних індивідуальних індексів співмножників. Наприклад, оскільки вартість (або товарообіг) дорівнює добутку ціни на фізичний обсяг, то

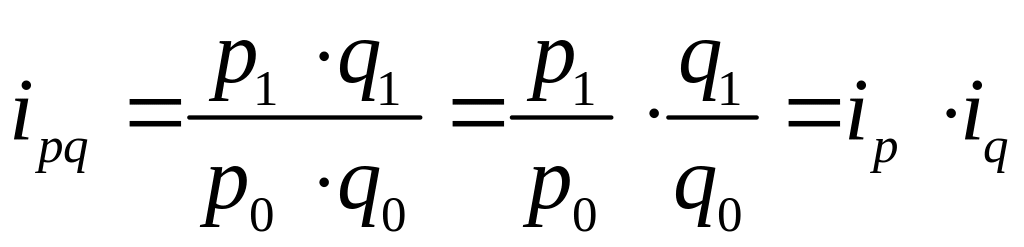. (5.1)

Ця залежність є формальним вираженням однієї із систем співзалежних індексів і в багатьох випадках має місце й для загальних індексів.

3. Якщо деякий показник є величиною, оберненою до іншого показника, то його індекс є величиною, оберненою до індекса цього іншого показника. Наприклад, якщо w – продуктивність праці (тобто фізичний обсяг продукції, що виробляється за одиницю часу), а t – трудомісткість продукції (тобто час, необхідний для вироблення одиниці продукції), то

,

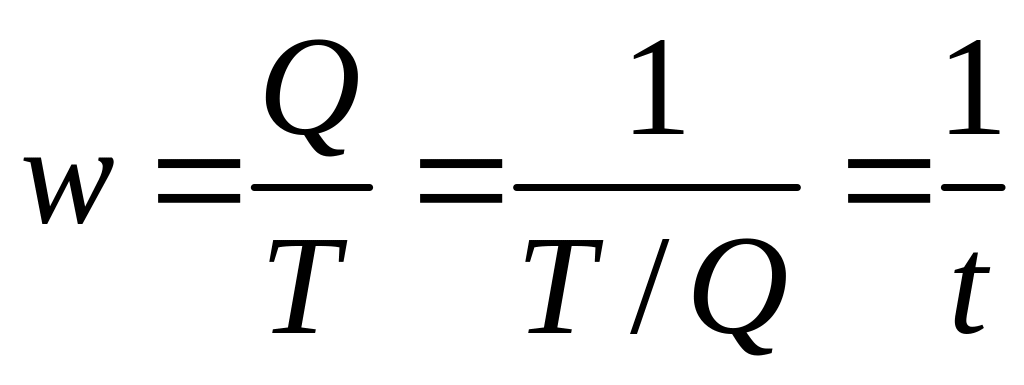де Q – фізичний обсяг продукції, виробленої за час Т. Тоді

.

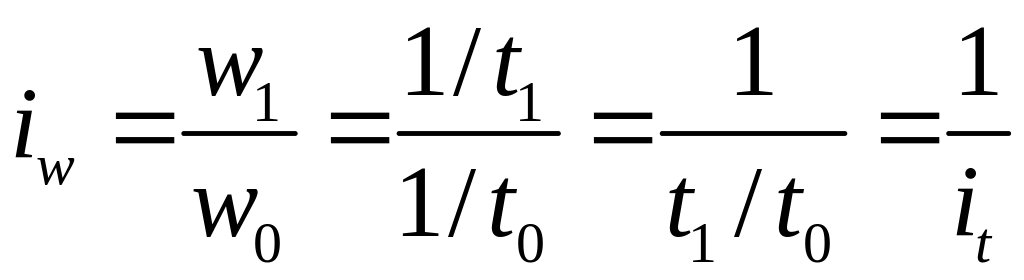У практиці статистичних досліджень наведені співвідношення між індексами можуть використовуватись для обчислення індексів або для контролю обчислень.

55. Методи обчислення: а) індивідуальних індексів; б) загальних індексів для однорідних об'єктів; в) загальних індексів для неоднорідних об'єктів (агрегатних індексів); г) загальних індексів у середньозваженій формі.

Ідивіуальні індекси=індексована величина у поточному періоді/індексовану величину у базовому періоді. Приклад:ip=p1/p0. З аналітичної точки зору індивідуальні індекси подібні темпам зростання, вони характеризують зміну індексованої величини у поточному році порівняно з базисним. Для характеристики таких показників як вартість, яка є добутком p*q використовуються агреговані індекси, чисельник і знаменник яких є добутком двох величин: ipq=p1q1/p0q0. Загальні індекси використовуються для виміру динаміки складного явища, яке може складатися з однорідних або неоднорідних явищ. Наприклад, якщо товари будуть мати різні одиниці вимірювання то вони будуть неоднорідними і механічне сумування їх показників буде помилковим. Критерій однорідності явищ не можна чітко сформулювати, проте в його основі повинні лежати мета дослідження і одиниці вимірювання явищ. Загальні індекси для однорідних об’єктів можна розраховувати за допомогою сумування відповідних кількісних показників у поточному і бозовому періоді. Iq=sum(q1)/sum(q0). Загальний індес ціни для однорідних об’єктів розраховується за індесом цін змінного складу Ip=p1середня/p0середня. Загальний індекс зміни вартості для однорідних об’єктів=Ipq=sum(p1*q1)/sum(p0*q0), Для розрахунку загальних індексів для неоднорідних об’єктів використовуються агрегатні індекси. Ip=sum(p1*q1)/sum(p0*q1)(фіксується фізичний обсяг для поточного періоду). Iq=sum(q1*p0)/sum(q0*p0)(фіксується ціна на базисному рівні). Загальний індекс вартості розраховується аналогічно, як і для однорідних об’єктів. Середньозважений індекс являє собою середній з індивідуальних індексів, зважених на товарообіг (вартість), зафіксований на одному рівні (базисному чи поточному). Використовуються тоді, коли є дані про ціну та обсяги продукції лише за один період (базисний чи поточний) та відповідні індивідуальні індекси, або дані про загальний товарообіг базового та поточного періодів і індивідуальні індекси ціни або фізичного обсягу. Тобто Ip=sum(ip*p0*q0)/sum(p0*q0)=sum(p1*q1)/sum(p1*q1/ip). Для фізичного обігу розраховуємо аналогічно лише з iq.