49. Аналітичне вирівнювання рядів динамікиАналітичне вирівнювання рядів динаміки, основні етапи побудови трендової кривої.

Аналіт вирівн є більш досконал сп обробки часових рядів, який дає можл не тільки гарантовано виявляти тенд, але й робити прогноз розв явища на наступні час мом або інтервали. Метод застосов для рівномір інтервал рядів і для мом рядів з довільними проміжками δ_і часу між мом.

Суть методу полягає в тому, що кожн фактичний рівень у_і розгл як сума двох доданків: , де – системати складова, яка відображ загальну тенденцію і вираж рівнянням =f(t); – вип складова, яка відображ флуктуації рівнів ряду .

Таким чином, аналіт вирів д ряду означ побудову ф-ції =f(t), яка аналіт вираж залеж систематич складової значень оз Y від часу t. Такі функції і їх графіки назив тренд кривими. За доп тренд кривої завжди можна встанов тенд розв яв, її хар-тер, а також зроб прогноз на наступні часові інтервали або моменти.

Процедура побуд трендової кривої скл з двох етапів: 1) вибір виду ф-ції f(t); 2) обчисл параметрів вибраної ф-ції.З мат точки зору побудова трендової кривої аналогіч побудові рівняння регрес, за винятком двох моментів:

1. Якщо ряд є рівномір і непер, то сист лін рівн можна спростити.необхідно: а) усі час мом t_i мом ряду пронумерув, починаючи з нуля, і надалі моменти t_i ототожнювати з їх номерами: t_i=і, і= ; б) перейти до умовних номерів , перенумерувавши часові інтерв або мом так, щоб точка відліку опин у сер часового ряду. 1.для непарного числа (п+1) рівнів ряду: =t_i – п/2 (n=2l, ),2.для парного числа (п+1) рівнів ряду: =2t_i – п (n=2l+1, ),

звідки , .

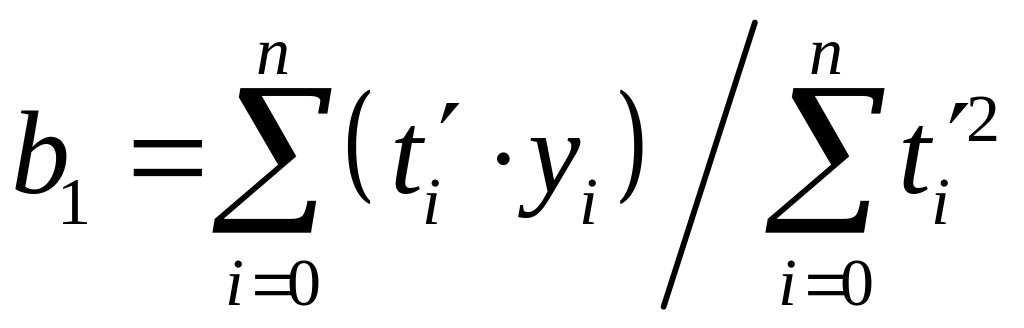звідки , що

Після розв сист одерж лінійну та квадрат моделі тренду та ,як ф-ції умов часу . Для перех до фактич часу t необхідно в рівняннях замість покласти: =t–l для непар числа рівнів ряду, де l=n/2; =2t–п для пар числа рівнів ряду. 2. Рег дисперс обчисл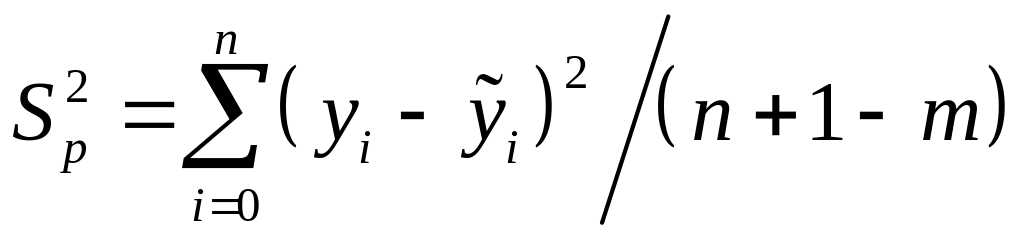 , де – вирів знач рівн ряду; (п+1) – число рівнів ряду; п – номер остан рівня ряду; т – число параметрів трендової кривої.

50. Поняття про періодичні коливання в рядах динаміки, аналітичне вирівнювання часових рядів у випадку наявності періодичних коливань.

У проц порівняння квартальних чи місяч даних багатьох соціально-ек яв часто виявляються періодичні коливання, що виник під впливом змін пори року. Вони є рез впливу кліматич умов, загальних ек факторів, а також багатьох інш факторів, які часто підлягають регулюв.

У широкому розумінні до сезон відносять всі явища, що виявл в своєму розв чітко виражену закономірність змін, що пов’язані зі змінами пори року, тобто більш-менш сталих коливань рівнів, які повторюються щорічно.

У статистиці періодичні коливання, що мають певний та постійний період, рівний річному проміжку, носять назву сезонних коливань або сезонних хвиль, а динаміч ряд в цьому вип назив сезонним рядом динаміки.

Сезонні коливання спостеріг в різних галузях економіки. Сезонні коливання, як правило, негативно вплив на рез виробнич діял, бо призводять до поруш ритмічності вир-ва. Комплексне регулюв сезонних змін в окремих галузях економіки повинно ґрунтуватися на дослідж сезонних коливань.

У стат існ низка методів вивч та виміру сезон коливань. Найпростіший полягає в побудові спеціал показників, які назив індексами сезонності . Сукупність цих показників відображ сезонну хвилю. Індексами сезонності є процентні віднош фактичних внутрішньогруп рівнів до теоретичних рівнів, що беруться за базу порівняння.

Для того, щоб виявити стійку сезонну хвилю, на якій не відображалися б випадкові умови одного року, індекси сезонності обчис за даними за кілька років, як правило, не менше трьох, що розподілені за місяцями. Якщо ряд динаміки не містить чітко вираж тенд розвитку, то індекси сезонності розрахов безпосередньо за емпіричними даними без їх попереднього вирівнюв.

Для кожного місяця розрахов середня вел-на рівня за кількістю обраних років за формулою: , де і – номер місяця (і = 1 12);j – номер року;m – кількість років.