
- •51. Особливості вимірювання взаємозв’язків в рядах динаміки.
- •59. Територіальні індекси.
- •1. Походження та основні значення терміну "статистика". Основні джерела статистики як науки
- •2. Предмет, методи та основні завдання статистики як науки.
- •3. Абсолютні та відносні, дискретні та неперервні величини у статистиці.
- •4. Статистичні показники та їх класифікація. Статистичні дані. Навести приклади.
- •5. Статистична сукупність. Поняття ознаки та її варіації. Приклади.
- •Ознака – це якісна особливість одиниці сукупності. Ознаки поділяються на дві групи:
- •6. Статистичні шкали та їх види, відповідна класифікація ознак. Приклади.
- •7. Основні етапи статистичного дослідження.
- •8. Статистичне спостереження. Загальний план спостереження та його структура.
- •9. Види і способи (класифікація) статистичних спостережень. Приклади.
- •10. Вимоги до результатів спостереження.
- •11. Контроль достовірності результатів та помилки спостереження.
- •12. Контроль достовірності результатів та помилки спостереження.
- •12. Статистичне зведення, його мета та складові частини
- •13. Статистичне групування, його види (класифікація)
- •14. Методика проведення групувань.
- •15.Статистичні таблиці. Їх види та правила оформлення.
- •16. Статистичні графіки та їх структура (складові частини)
- •17. Види (класифікація) стат-х графіків. Приклади
- •18.Поняття про ряд розподілу. Види рядів розподілу. Приклади
- •19. Графічне зображення варіаційних рядів розподілу. Полігон, гістограмма, кумулята. Приклади.
- •20. Середня варіаційного ряду. Основні види степеневих середніх. Правило мажорантності. Властивості середньої арифметичної.
- •21. Мода варіаційного ряду. Визначення та способи обчислення моди для звичайного, дискретного та інтервального варіаційних рядів.
- •22. Медіана варіаційного ряду. Визначення та способи обчислення медіани для звичайного, дискретного та інтервального варіаційних рядів.
- •24. Поняття форми розподілу, вершини розподілу. Поділ варіаційних рядів на види за формою. Приклади.
- •25. Симетричність розподілу, види асиметрії. Попередні ознаки симетричності та виду асиметрії. Наближені та точні числові характеристики асиметрії. Вимірювання величини асиметрії.
- •26. Гостро- та плосковерхість розподілу, візуальні можливості їх встановлення. Числова характеристика гостро- та плосковерхості. Однорідність статистичної сукупності.
- •27. Основні поняття та основні задачі вибіркового спостереження. Репрезентативність вибірки, основні види помилок репрезентативності.
- •28. Основні схеми та види відбору, їх переваги, недоліки та можливі застосування.
- •29. Точкові та інтервальні оцінки параметрів генеральної сукупності. Поняття надійних інтервалу та ймовірності.
- •31. Визначення мінімально необхідного обсягу вибірки
- •32. Основні види взаємозалежності між ознаками, їх основна характеристика.
- •33.А)Метод комбінаційного групування
- •35.В)Дисперсійний аналіз
- •36.Г)Вибір виду рівняння регресії та обчислення його параметрів (регресійний аналіз):
- •37.Д)Оцінювання істотності та вимірювання щільності зв'язку за допомогою коефіцієнту детермінації (кореляційний аналіз):
- •38.Е)Оцінювання істотності і вимірюв щільності лінійного зв'язку за доп лінійного коефіцієнта кореляції, його зв'язок з коефіцієнтом детермінації:
- •39.Ж)Метод кореляції знаків Фехнера
- •40.З)Метод кореляції рангів Спірмена.
- •41. Порівняльний аналіз методів дослідження взаємозв'язків.
- •42. Поняття про ряд динаміки, види динамічний рядів.
- •43.Порівнюваність рівнів і змикання часових рядів.
- •45. Характеристики динаміки рівнів часового ряду: а) абсолютний приріст; б) темп зростання; в) темп приросту;
- •46. Поняття тенденції динамічного ряду, види і характери тенденцій.
- •47. Виявлення виду та характеру тренду динамічного ряду за допомогою порівняння рівнів ряду та аналізу його абсолютних приростів.
- •48. Основні методи згладжування рядів динаміки: а) метод середньої плинної; б) укрупнення інтервалів.
- •49. Аналітичне вирівнювання рядів динамікиАналітичне вирівнювання рядів динаміки, основні етапи побудови трендової кривої.
- •50. Поняття про періодичні коливання в рядах динаміки, аналітичне вирівнювання часових рядів у випадку наявності періодичних коливань.
- •52.Інтерполяція та екстраполяція. Точкове та інтервальне прогнозування часових рядів.
- •54. Основні залежності між індексами.
- •56. Індексний факторний аналіз.
- •57. Індекси середніх величин.
- •58. Міжгрупові індекси.
- •59. Територіальні індекси.
42. Поняття про ряд динаміки, види динамічний рядів.
У найпростішому випадку рядом динаміки (або динамічним рядом, або часовим рядом) називається сукупність не менше трьох пар чисел (ti; уі), розташованих у порядку зростання ti, де ti – час (момент або інтервал), уі – відповідне значення показника, який характеризує явище, що вивчається; числа уі зазвичай називають рівнями ряду динаміки.
Вищеозначені динамічні ряди можна класифікувати за такими основними ознаками:
За видом часу: а) інтервальні – час ti являє собою певний часовий проміжок; б) моментні – час ti являє собою певний момент часу.
За типом показника: а) абсолютних величин; б) відносних величин; в) середніх величин.
За рівномірністю часу: а) рівномірні ряди – всі часові інтервали для інтервального ряду або проміжки часу між моментами для моментного ряду рівні між собою або вважаються рівними; б) нерівномірні ряди – хоча б два часових інтервали або проміжки часу між моментами не рівні між собою.
За неперервністю часу: а) неперервні ряди – не мають пропусків рівнів ряду; б) розривні ряди – мають пропуски рівнів ряду.
Загальний вид найпростішого ряду динаміки
і |
0 |
1 |
2 |
… |
п |
ti |
t0 |
t1 |
t2 |
… |
tп |
уі |
у0 |
у1 |
у2 |
… |
уп |
Для наочності часовий ряд можна зображ графічно. Графік динаміч ряду являє собою сукупн точок з координатами (ti; уі), побудов у прямокутній системі координат toy і послідовно сполуч відрізками прямих. Вищезгадану сукупність точок назив кореляц полем.
Для нерівномірних інтервальних рядів кореляційне поле і, відповідно, графік ряду не визначаються і не будуються.
43.Порівнюваність рівнів і змикання часових рядів.
Дослідження часових рядів з непорівняними рівнями не має сенсу.
Основні причини неможливості порівняння рівнів:
зміна територій, до якої відносяться показники, значення яких є рівнями ряду;
зміна дат обліку даних;
зміна методик обліку або обчислень значень рівня ряду;
зміна ціни для варіаційних показників;
різна довжина інтервалів в інтервальному ряді динаміки.
При дослідженні часового ряду необхідно переконатись в можливості порівняння рівнів цього ряду, якщо порівнюваність не забезпечена або її не існує, треба її забезпечити (залежно від причин).
Питання про порівнянність рівнів виникає при змиканні часових рядів.
Змикання часових рядів
Змиканням рядів динаміки називається об’єднання в один ряд двох або декількох рядів, рівні яких являють собою значення одного й того ж показника, але задані на різних часових інтервалах або моментах і з певних причин є не порівняльними. При цьому змикання декількох рядів проводиться попарно. Всі ряди, що змикаються, повинні бути тільки момент ними або тільки інтервальними. При змиканні інтервальних рядів останні повинні бути рівномірними. Якщо ряди, що змикаються, мають різну довжину інтервалів, то інтервали можна вирівняти способом, аналогічним процедурі рівномірізації нерівномірного інтервального ряду.
Метою змикання часових рядів є забезпечення порівнюваності рядів одержаного ряду.
Процедура змикання двох рядів полягає в тому, що значення рівнів одного з рядів, який будемо називати змінюваним, пере обчислюється так, щоб вони стали порівняними з рівнями іншого ряду, який будемо називати змінюючим. Після цього обидва ряди об’єднуються в один ряд, який будемо називати зімкненим.
Однією з умов можливості змикання двох часових рядів є наявність значень рівнів в обох рядах для одного й того ж часового інтервалу або моменту, який будемо називати перехідним. В цьому випадку змикання двох часових рядів можна проводити одним з двох способів, які є способами пере обчислення значень рівнів змінюваного ряду.
1. Метод додавання. Полягає в тому, що до кожного рівня хі змінюваного ряду Х додається число Δе , що дорівнює уе-хе, де уе та хе – рівні відповідно змінюючого ряду у та змінюваного ряду х для перехідного часового ряду або моменту. В результаті кожний рівень kі’ зміненого ряду У’ обчислюється за формулою: хі’=х+ Δе.
2. Метод множення. Полягає в тому, що кожний рівень хі змінюваного ряду Х треба помножити на число ke, яке дорівнює
ke =уе/хе, уе - рівень змінюючого ряду, хе - рівень змінюваного ряду.
В результаті кожний рівень хі’ зміненого ряду Х’ обчислюється за формулою хі’=хі+ kе. Δе. – різниця переходу, kе – коефіцієнт переходу.
44. Основні числові характеристики часових рядів можна розділити на три групи: а) характеристики центру рівнів ряду; б) характеристики варіації рівнів ряду; в) характеристики динаміки рівнів.
До першої групи відноситься середній рівень ряду, який визначається і обчислюється в залежності від виду часового ряду.
Середній рівень ряду динаміки є однією з узагальнюючих його характеристик і зазвичай позначається . Визначення і, відповідно, формули для обчислення залежать від типу динамічного ряду.Для інтервальних рівномірних неперервних часових рядів визначається як середнє значення ознаки Y за один часовий інтервал протягом усього часу спостереження і обчислюється як середня арифметична рівнів ряду:
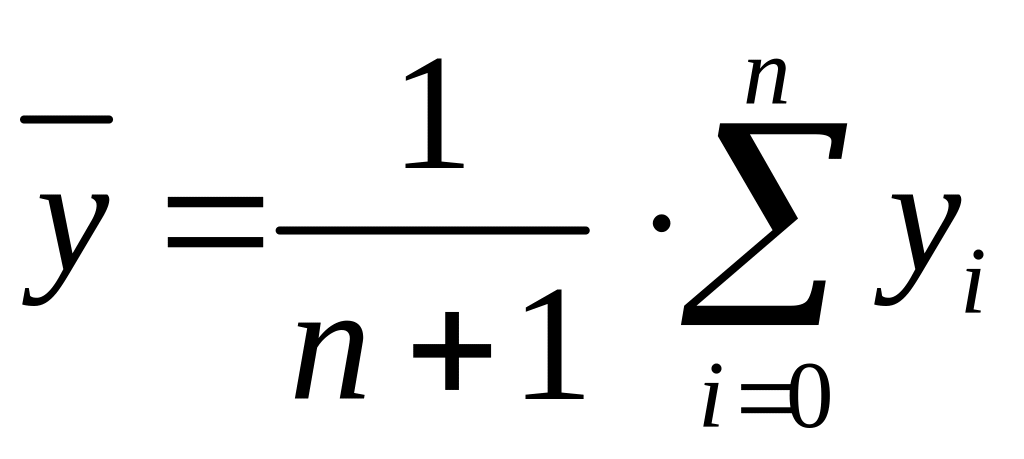 .Для
інтервальних
нерівномірних
часових рядів середній рівень ряду не
визначається і, відповідно, не обчислюється.
.Для
інтервальних
нерівномірних
часових рядів середній рівень ряду не
визначається і, відповідно, не обчислюється.
Для моментних часових рядів називається середньою хронологічною і визначається як висота прямокутника з основою, що дорівнює (tn–t0), рівновеликого криволінійній трапеції, яка обмежена графіком часового ряду (рис. 4.1), віссю оt і прямими t=t0 та t=tn. Із наведеного визначення витікає, що
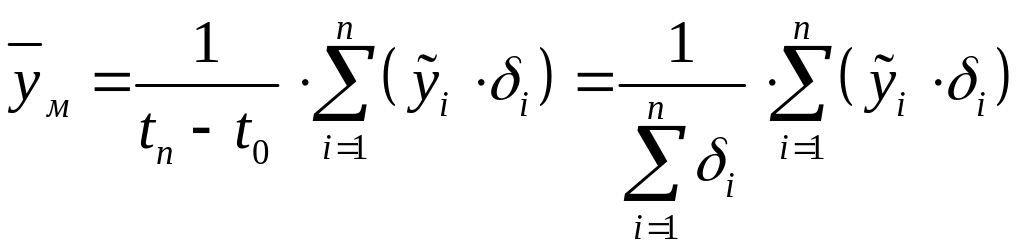 ,де
,де
![]() .
.
Головними характеристиками другої групи є: дисперсія, середнє квадратичне відхилення, коефіцієнт осциляції та квадратичний коефіцієнт варіації рівнів ряду.:
дисперсія

середнє квадратичнє відхилення
![]() ,
,
квадратичний коефіцієнт варіації, який може виражатись відношенням або у процентах за формулами відповідно
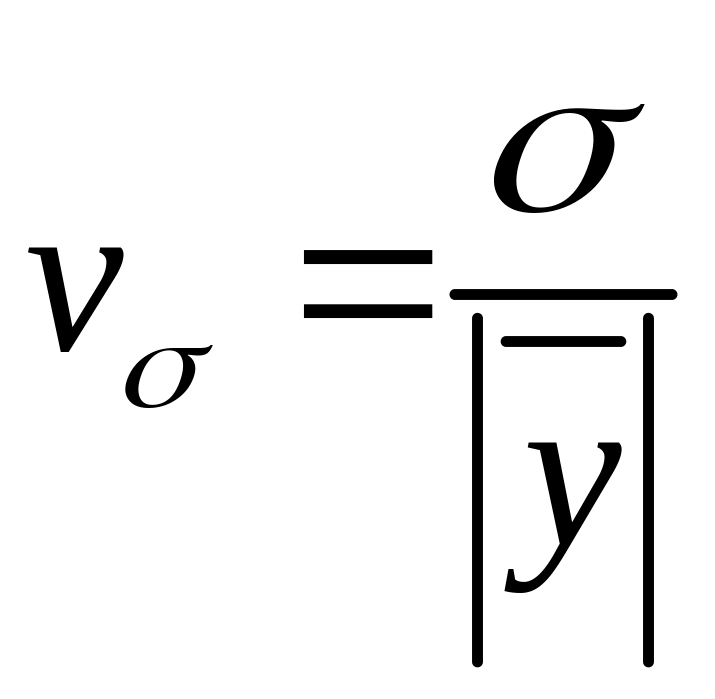 ;
;  ,
,
коефіцієнт осциляції, який може виражатись відношенням або у процентах за формулами відповідно
 ;
;
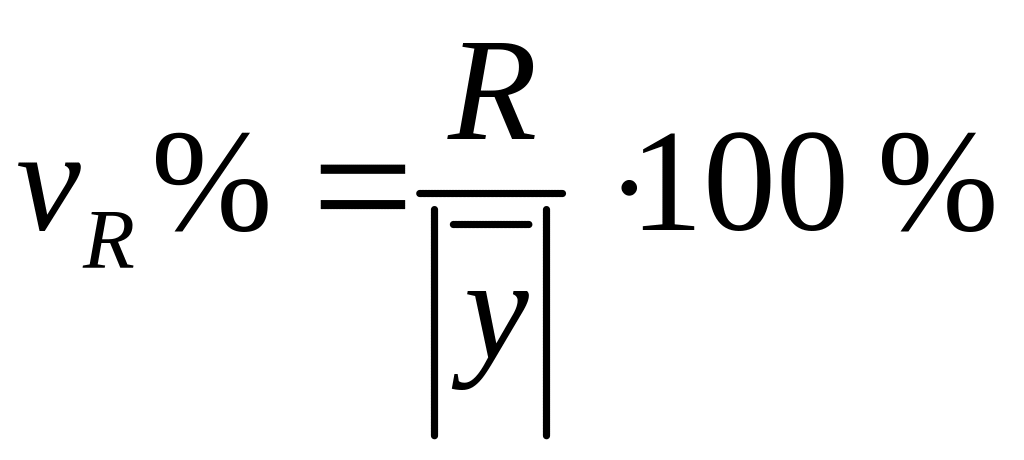 ,
,
де
![]() –
розмах варіації рівнів ряду.
–
розмах варіації рівнів ряду.
