40.З)Метод кореляції рангів Спірмена.

Числовою мірою істотності та щільності зв’язку в даному методі є коефіцієнт кореляції рангів Спірмена

,

де d_i=u_i–v_i – різниця рангів u_i та v_i для відповідно х_і та у_і, п – число пар (х_і; у_і). Можна показати, що [‑1; 1].

Рангом u_i(v_i) кожного значення х_і(у_і) є його порядковий номер, якщо всі х_і(у_і) розташувати у неспадному порядку. Якщо при цьому деякі значення х_і(у_і) збігаються, то кожному з них присвоюється ранг, що дорівнює середньому арифметичному їх фактичних порядкових номерів.

Для перевірки істотності зв’язку необхідно за формулою обчислити спостережене значення величини і порівняти його модуль з критичним значенням , яке залежить від обсягу сукупності п та рівня значущості α і знаходиться за формулою: ,

де − рівень значущості; − число степенів вільності; − обсяг вибірки; − критична точка розподілу Стьюдента для двосторонньої критичної області.

Якщо , то зв’язок вважається істотним з імовірністю γ=( ) і навпаки. Рівень значущості зазвичай вибирається рівним 0,05 або 0,10 і являє собою імовірність ризику визнати зв’язок істотним, коли він насправді не існує.

Якщо зв’язок буде визнано істотним, то його щільність можна оцінювати за правилом трисекції:

• для 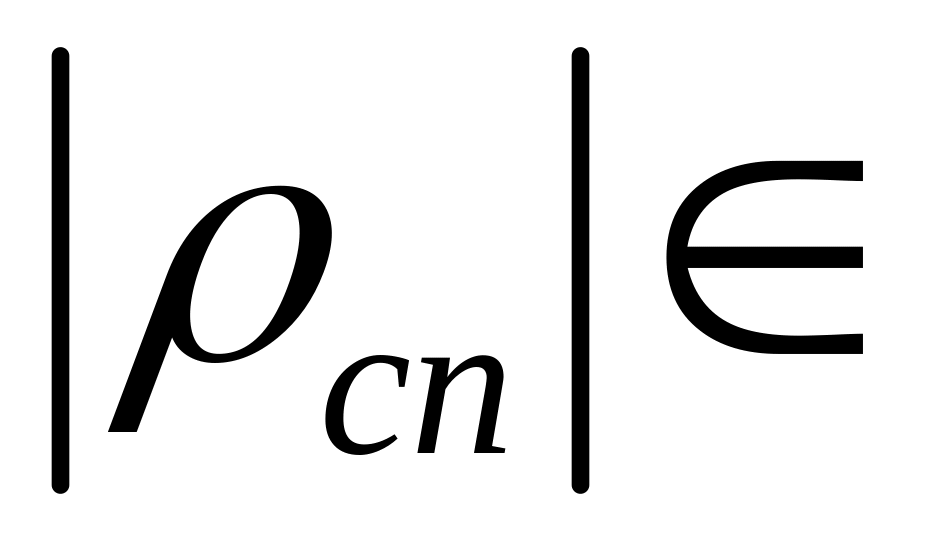(0,3 + 0,7; 1] зв’язок вважаємо щільним;

• для (0,7 + 0,3; 0,3 + 0,7] – помірним;

• для ( ; 0,7 + 0,3] – слабким.

Знак визначає напрям залежності: якщо , то зв’язок прямий і навпаки.

41. Порівняльний аналіз методів дослідження взаємозв'язків.

Метод комбінаційного групування:

а) може застосов у вип, коли обидві ознаки (або одна з них) є атрибутивними або варіаційними;

б) дає можл формально перевіряти істотність та оцінювати щільність зв’язку, а також визнач його напрям, якщо оз варіац або атрибутивні рангові;

в) не дає можл визнач вид і характер зв’язку.

Метод аналітичного групування

а) може застосов у вип, коли факторна ознака є атрибутивною або варіаційною, а результативна – тільки варіаційною;

б) дає можл тільки припускати наявність або відсутність зв’язку, а також визначати його напрям та можливий вид і характер залежності.

в) не дає можл формал перевіряти істотність та оцінюв щільність зв’язку.

Метод дисперсійного аналізу.

а) може застосов у вип, коли факторна оз є атрибутивною або варіац, а рез – тільки варіац;

б) дає можл формально перевіряти істотність звязку та оцінюв його щільність;

в) не дає можл визнач напрям, характер та можливий вид залежності.

Метод КРА:

а) застосов у випадках, коли обидві ознаки є варіаційними;

б) дає можл формально перевіряти істотність та оцінювати щільність зв’язку, а також знах аналітичний вид залежності, її напрям та характер.

У КРА лінія регресії задається аналітично, шукається у вигляді рівняння ,рівняння регресії.

Метод кореляції знаків Фехнера:

а) застосов у вип, коли обидві оз є варіаційними;

б) дає можл формально, але наближено оцінюв істотність та щільність залежності, а також визнач її напрям;

в) не дає можл визнач вид та характер зв’язку.

Метод збігу знаків є одним з найбільш простих методів і вимагає обчислення тільки загальних середніх та ознак відповідно Х та Y.

Метод кореляції рангів Спірмена:

а) застосовується у вип, коли обидві оз (або одна з них) є атрибутивними або варіаційними, але шкала атрибутивної оз може розглядатись як рангова;

б) дає можл формально перевіряти істотність і оцінюв щільність зв’язку, а також визнач його напрям;

в) не дає можл визнач вид та характер залежності.

Даний метод належить до так званих непараметричних методів наближеного оцінюв зв’язку, оскіл його застосув не потребує обчислення будь-яких параметрів сукупності, що вивчається.