35.В)Дисперсійний аналіз

Для реалізації методу необхідно:

1. Усю сукупність п пар (х_і; у_і) розділити за факторною оз на т груп (інтервалів) з обсягом (або частотою) f_k кожної групи. Для варіаційної факторної оз ширина інтервалів обирається дослідником суб’єктивно, бажано, щоб інтервали були кількісно однорідними і т 3.

2. Обчисл загальну середню рез оз Y для всієї сукупності:

та групові середні для кожної k-ї групи : .

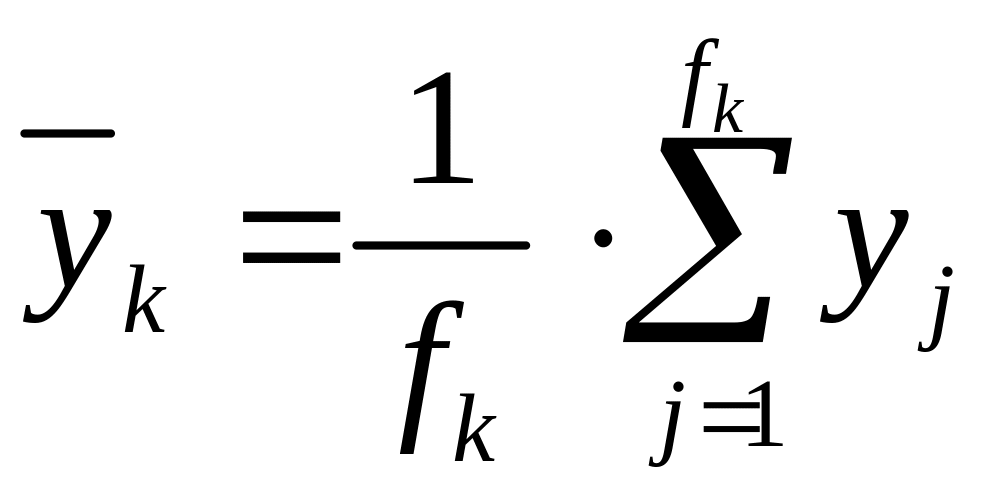3. Обчислити загал дисперсію ознаки Y для всієї сукупності:

,

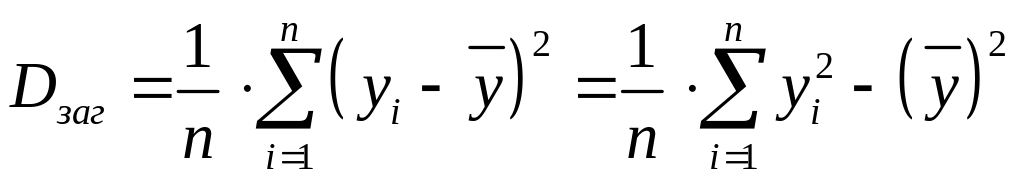групові дисперсії для кожної k-ї групи: ,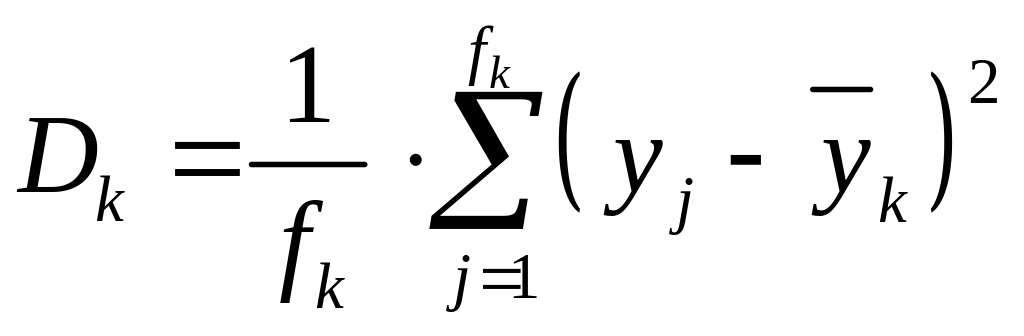

середню зважену з групових дисперсій: ,

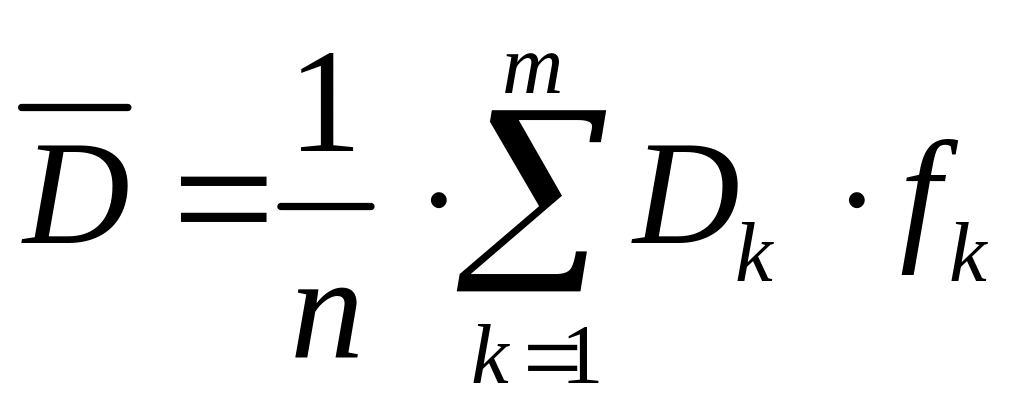де f_k – частота k-ї групи,

міжгрупову дисперсію: .

Для вищенаведених величин існ правило додавання дисперсій:

.

4. Обчислити величину

,

яка називається кореляційним відношенням і є числовою мірою щільності та істотності зв’язку в дисперсійному аналізі. Очевидно, що  [0; 1].

5. За таблицями критичних значень величини η² знайти її критичне значення , яке залежить від рівня значущості α та степенів вільності k₁=m‑1 i k₂=n‑m. У статистичній практиці величина α вибирається зазвичай рівною 0,05 або 0,10 і являє собою імовірність оцінити зв’язок як істотний при його фактичній відсутності.

6. Порівняти з критичним і зробити висновок: якщо > , то з імовірністю γ=(1–α) зв’язок вважається істотним (тобто, існуючим) і навпаки.

7. Для оцінки щільності зв’язку можна керуватись правилом трисекції: будемо вважати зв’язок:щільним для  (0,3 + 0,7; 1];помірним для  (0,7 + 0,3; 0,3 + 0,7];слабким для  ( ; 0,7 + 0,3].

36.Г)Вибір виду рівняння регресії та обчислення його параметрів (регресійний аналіз):

У статистичній практиці найбільш поширеними видами рівнянь регресії є такі, параметри яких мають певний фізичний зміст, зокрема:

1. Лінійна залежність а+bх. 2. Квадратична залежність р+qx+rx².

Вибір виду рівняння регресії в кожному конкретному дослідженні залежить, в основному, від двох факторів: 1) виду кореляційного поля, яке в даному випадку являє собою сукупність точок з координатами (х_і; у_і) ( ), побудованих в прямокутній системі координат хоу; 2) ретельного вивчення суті явища, що досліджується, з урахуванням результатів попередніх аналогічних досліджень, якщо останні проводились.

Можлива ситуація, коли ні аналіз явища, ні вигляд кореляційного поля не дають можливості однозначно вибрати вид рівняння регресії. В такому випадку необхідно вибрати дві (або більше) найб адекватні функції, провести для кожної повне дослідж і за їх рез вибрати одну, кращу. При цьому можна формалізувати вибір, обираючи, наприклад, ту залежність, для якої рег дисперсія буде меншою за інш.

Параметри рівняння регресії f(x) зазвичай знаходяться за методом найменших квадратів, який забезпечує такий вибір їх числових значень, щоб сума квадратів відхилень емпіричних значень у_і ознаки Y від відповідних знач f(x_і) була найменшою.

Зокрема, для лінійного а+bх та квадратичного р+qx+rx² рівнянь регресії параметри знах із сист лінійних алгебраїч рівнянь відповідно

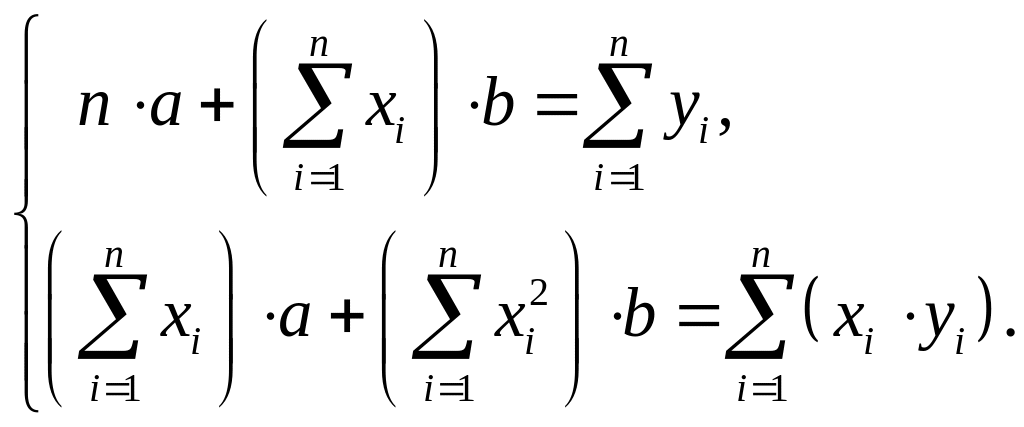
та

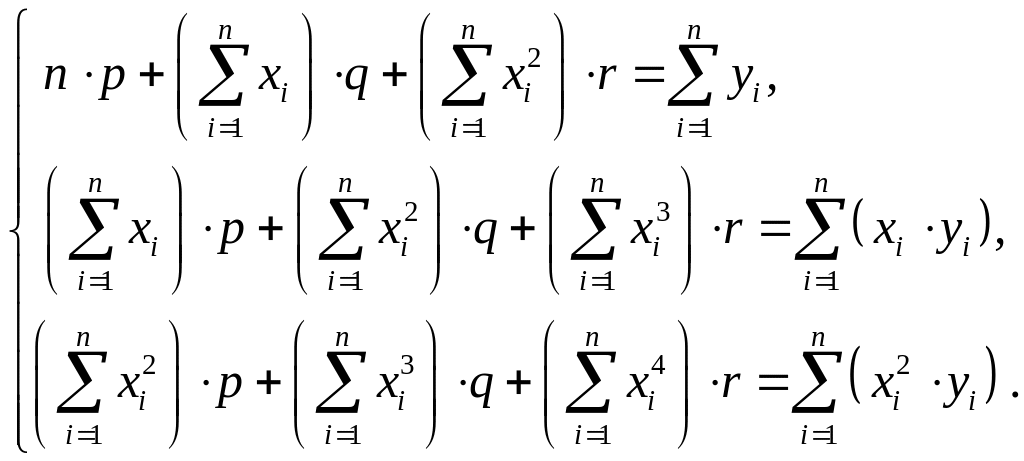
Величина , де п – число пар (х_і; у_і), m – число параметрів рівняння регресії, які знах за даними вибірки, назив рег дисперсією і може слугувати критерієм вибору виду рівняння регресії.

Для перевірки рівнянь необхідно побудувати їх графіки на кореляційному полі і візуально переконатись у тому, що точки (х_і; у_і) кореляційного поля розташовані хоча б приблизно порівну і рівномірно по обидва боки графіка.