26. Гостро- та плосковерхість розподілу, візуальні можливості їх встановлення. Числова характеристика гостро- та плосковерхості. Однорідність статистичної сукупності.
Під формою розподілу варіаційного ряду у статистиці розуміють форму його графічних зображень: полігону або гістограми. За своєю формою всі варіаційні ряди розподілу поділяються на: одновершинні і багатовершинні, симетричні та асиметричні, гостроверхі й плосковерхі.
Гостроверхість чи плосковерхість розподілу встановлюється відносно теоретичного нормального розподілу неперервних випадкових величин з тим же значенням дисперсії σ2 і визначається за допомогою коефіцієнта ексцесу, який у статистиці визначається як відношення центрального моменту четвертого порядку до четвертого степеня середнього квадратичного відхилення: Ех=μ4 /σ4 і обчислюється для д. в. р. та і. в. р. за формулами відповідно:
;
.
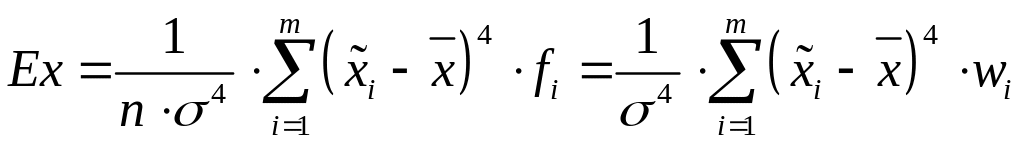Для теоретичного нормального розподілу Ех=3, тому якщо Ех>3 (Ех<3), то розподіл вважається гостроверхим (плосковерхим). Величина гостро- чи плосковерхості в статистиці не вимірюється.
Кількісна однорідність статистичної сукупності
Будемо вважати статистичну сукупність кількісно однорідною, якщо відповідний розподіл є унімодальним та одновершинним.
Якщо виконується тільки одна з вищезазначених умов (очевидно, що перша), то статистичну сукупність вважатимемо частково однорідною.
Якщо не виконується жодна з вищенаведених умов, то статистичну сукупність вважатимемо неоднорідною.
Для однорідної статистичної сукупності всі результати досліджень і зроблені висновки вважаються досить надійними, а обчислені числові характеристики – типовими, тобто такими, що досить точно репрезентують відповідні характеристики генеральної сукупності, з якої вибрана дана статистична сукупність.
Проведення статистичних досліджень для неоднорідної сукупності формально є некоректним, але в статистичній практиці все ж таки допускається в разі необхідності. При цьому будь-які результати досліджень слід вважати менш надійними і типовими.
27. Основні поняття та основні задачі вибіркового спостереження. Репрезентативність вибірки, основні види помилок репрезентативності.
Вибіркове спостереження проводиться тоді, коли проведення суцільного спостереження неможливе або недоцільне і являє собою науково обґрунтований спосіб несуцільного спостереження, при якому досліджується лише незначна частина сукупності, що вивчається, відібрана за певними правилами. Правила відбору повинні забезпечувати одержання результатів, які адекватно характеризують всю сукупність, що вивчається.
Сукупність, що вивчається і з якої проводиться відбір, називається генеральною сукупністю. Відібрана її частина, що безпосередньо досліджується, називається вибірковою сукупністю або вибіркою.
Числові характеристики вибірки приймаються як оцінки відповідних числових характеристик (далі – характеристика) генеральної сукупності. Очевидно, що вибіркові характеристики не можуть точно збігатися з відповідними генеральними характеристиками. Розбіжності між ними називаються помилками репрезентативності й поділяються на дві основні групи: систематичні й випадкові.
Систематичні помилки ‑ результат порушення правил відбору і, зазвичай, мають односторонній характер. Тому їх іноді називають помилками зміщення, а відповідні характеристики – зміщеними. При правильному формуванні вибіркової сукупності систематичні помилки можуть бути виключені (або майже виключені).
Випадкові помилки ‑ результат заміни дослідження генеральної сукупності дослідженням вибірки і тому неминучі, але на відміну від систематичних помилок не мають одностороннього (тенденційного) характеру, тому не призводять до зміщення оцінок.
Вибірка може вважатись репрезентативною (або представницькою), якщо її структура (пропорції, частки і т. ін.) загалом збігається зі структурою відповідної генеральної сукупності. Для забезпечення репрезентативності вибірки необхідно: а) надати кожній одиниці генеральної сукупності рівні шанси потрапити у вибірку; б) обсяг вибірки повинен бути досить великим.
Основні завдання вибіркового спостереження: а) знаходження точкових й інтервальних оцінок параметрів генеральної сукупності; б) визначення мінімально необхідного обсягу вибірки для одержання інтервальних оцінок із заданою точністю та надійністю; в) визначення імовірності (або надійності), з якою заданий інтервал накриває параметр, що оцінюється.