21. Мода варіаційного ряду. Визначення та способи обчислення моди для звичайного, дискретного та інтервального варіаційних рядів.

Варіаційний ряд може не мати моди, мати одну моду (унімодальний в. р.) або декілька мод (мультимодальний в. р.). Зокрема, якщо моди дві, то в. р. – бімодальний. Мода, якщо вона існує, завжди є одним із можливих значень відповідної ознаки.

Модою з. в. р. у₁, у₂, …, у_п називається варіанта, яка найчастіше зустрічається в даному в.р.: Мо=у_е, якщо варіанта у_е найчастіше зустрічається в даному в.р. знаходиться візуально без будь-яких обчислень.Якщо всі варіанти даного з. в. р. зустрічаються однаково часто, то прийнято вважати, що останній не має моди.

Модою д. в. р. називається варіанта, частота або частка якої є найбільшою: Мо=х_е, якщо f_e ≥ f_i або w_e ≥w_i (i= ). знаходиться візуально з таблиці або полігону даного д. в. р.  Якщо всі частоти або частки д. в. р. однакові, то прийнято вважати, що останній не має моди.Модою і. в. р. називається статистичний аналог і точкова оцінка моди генеральної сукупності, з якої вибрана статистична сукупність, що згрупована в даний і. в. р. При цьому, якщо відповідна ознака є дискретною, то значення моди, обчислене за нижченаведеними формулами, округлюється до найближчого цілого числа.

Для обчислення моди і. в. р. спочатку знаходимо модальний інтервал (інтервали), яким є інтервал з найбільшою частотою або часткою.

Якщо і. в. р. має один модальний інтервал або декілька ізольованих (тобто, несусідніх) модальних інтервалів, то для кожного з них мода знаходиться за формулою:

, (1.4)

де х_Мо – нижня межа модального інтервалу, f_Mo (w_Mo) – частота (частка) модального інтервалу, f_Mo-1 (w_Mo-1) – частота (частка) інтервалу перед модальним, f_Mo+1 (w_Mo+1) – частота (частка) інтервалу після модального, k=1.

Якщо і. в. р. має групу сусідніх модальних інтервалів, то для кожної з них знаходиться одна мода за формулою (1.4), де х_Мо – нижня межа крайнього лівого з модальних інтервалів даної групи, k – кількість модальних інтервалів даної групи, f_Mo-1 (w_Mo-1) – частота (частка) інтервалу перед даною групою модальних інтервалів, f_Mo+1 (w_Mo+1) – частота (частка) інтервалу після даної групи модальних інтервалів.

Якщо модальним виявиться перший або останній інтервал (байдуже, ізольований чи сусідній), то у формулі (1.4) відповідно f_Mo-1=w_Mo-1 = 0 або f_Mo+1=w_Mo+1 = 0.

Якщо частоти або частки всіх інтервалів даного і. в. р. однакові, то прийнято вважати, що останній не має моди.

22. Медіана варіаційного ряду. Визначення та способи обчислення медіани для звичайного, дискретного та інтервального варіаційних рядів.

Варіаційний ряд завжди має єдину медіану, значення якої може бути або не бути одним з можливих значень відповідної ознаки.

Медіаною з. в. р. у₁, у₂, …, у_п називається число Ме, яке ділить останній на дві рівні за обсягом частини.якщо п=2k+1 – непарне число ( ), то Ме=у_k+1;якщо п=2k – парне число, то Ме=(у_k+у_k+1)/2.При цьому очевидно, що якщо з. в. р. побудований для дискретної ознаки, то для парного числа п медіана не є однією з варіант даного з.в.р. В інших випадках медіана є однією з варіант даного з.в.р.

Медіаною д. в. р. називається медіана відповідного з. в. р.

Для знаходження медіани д. в. р. спочатку необхідно для кожної його варіанти х_k обчислити її накопичену (або кумулятивну) частоту S_k (частку T_k):

.

При цьому можливі такі два випадки:

1. Для жодної з варіант S_k≠п/2 (T_k ≠1/2). Тоді медіаною д. в. р. буде перша з варіант х_k, для яких S_k >п/2 (T_k >1/2).

2. Для деякої k-ї варіанти S_k=п/2 (T_k=1/2). Очевидно, що це можливо тільки у випадку, коли n=2l – парне число (lєN). Тоді Ме = (х_k+x_k+1)/2.

Медіаною і. в. р. називається таке число Ме, для якого вертикальна пряма, що проходить через точку х=Ме, ділить гістограму частот або часток даного і. в. р. на дві рівновеликі частини.Для знаходження медіани і. в. р. спочатку необхідно для кожного k-го його інтервалу обчислити накопичену (або кумулятивну) частоту S_k (частку T_k) за формулою (1.5). Після цього знаходять медіанний інтервал, яким буде перший з інтервалів, для яких S_k>п/2 (T_k>1/2). Тоді медіана і. в. р. обчислюється за формулою:

,

де х_Ме – нижня межа медіанного інтервалу, f_Me (w_Me) – частота (частка) медіанного інтервалу, S_Me-1 (T_Me-1) – накопичена частота (частка) інтервалу перед медіанним.

23. Характеристики варіації ознаки у варіаційних рядах розподілу: а) розмах варіації, дисперсія, середні квадратичне та лінійне відхилення; б) коефіцієнти осциляції та варіації квадратичний та лінійний.

Розмахом варіації з. в. р. і д. в. р- різниця між найбільшим і найменшим значеннями варіант відповідно у_і (і= ) та х_k (k= ):R_у = y_n – y₁; R_х = x_m – x₁.

Розмахом варіації і. в. р. називається різниця між правою межею останнього (т-го) і лівою межею першого інтервалів: .

Дисперсією з. в. р. і д. в. р. називається середня квадратів відхилень варіант відповідно у_і (і= ) та х_k (k= ) від середньої відповідно та :

.

Дисперсією і. в. р. називається середня квадратів відхилень середин інтервалів (і= ) від середньої :

.

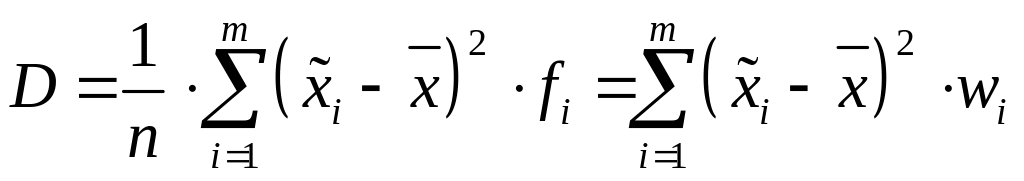Середнім квадратичним відхиленням варіаційного ряду називається квадратний корінь із дисперсії:

Середнім лінійним відхиленням з. в. р. і д. в. р. називається середня модулів відхилень варіант відповідно у_і (і= ) та х_k (k= ) від середньої відповідно та :

.

Середнім лінійним відхиленням і. в. р. називається середня модулів відхилень середин інтервалів (і= ) від середньої :

.

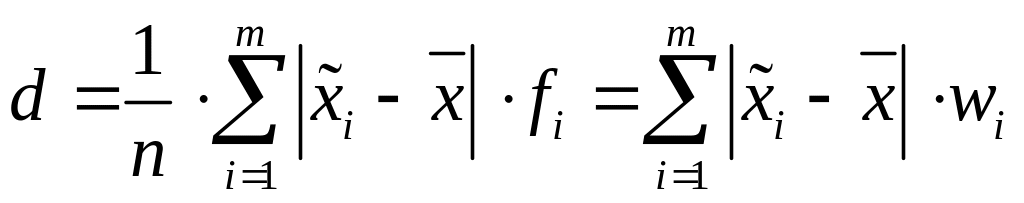Квадратичним (лінійним) коефіцієнтом варіації варіаційного ряду називається відношення середнього квардатичного (лінійного) відхилення до модуля середньої. Може виражатись відношенням або в процентах:

або .

Доведено, що для одного і того ж варіаційного ряду V_d <V_σ; якщо , то розподіл статистичної сукупності має бути близьким до симетричного

Коефіцієнтом осциляції варіаційного ряду називається відношення розмаху варіації до модуля середньої. Може виражатись відношенням або у процентах:

або .