
- •Отношение делимости. Свойства. Теорема о делении с остатком.
- •Глава 1. Делимость в кольце целых чисел §1. Отношение делимости
- •§2. Теорема о делении с остатком
- •Нод и нок целых чисел. Свойства. Алгоритм Евклида.
- •§3. Нод и нок, алгоритм Евклида
- •Взаимно простые числа. Их свойства. Простые и составные числа. Основное свойство простых чисел.
- •§5. Взаимно простые числа
- •§6. Простые и составные числа Основная теорема арифметики
- •Бесконечность множества простых чисел. Критерий простоты числа. Основное свойство простых чисел
- •§8. Теорема Евклида
- •Основная теорема арифметики и следствия из нее.
- •Сравнения и их свойства.
- •§ 1. Сравнения и их основные свойства.
- •Классы вычитов. Полная и приведенная система вычитов.
- •§ 2. Полная и приведенная система вычетов по модулю m.
- •§ 3. Кольцо классов вычетов.
- •8.Функция Эйлера. Вывод явной формулы для функции Эйлера. Теоремы Эйлера и Ферма.
- •§ 4. Функция Эйлера
- •§ 5. Теоремы Эйлера и Ферма
- •9. Сравнения и системы сравнений с неизвестной величиной.
- •§1. Решение сравнений. Равносильные сравнении
- •§3. Системы сравнений
- •10. Сравнения 1-й степени. Неопределённые уравнения
- •§ 2. Сравнения 1-й степени. Неопределённые уравнения
- •11. Сравнения по простому модулю. Сравнения по степени простого числа. Сравнения по составному модулю.
- •§4 Сравнении с неизвестной величиной по простому модулю
- •§5. Сравнения по составному модулю
- •§6. Сравнения но модулю рn
- •§7. Двучленные сравнения. Квадратичные вычеты и невычеты
- •12. Показатели чисел и классов вычетов по данному модулю
- •§1. Показатели классов и чисел по данному модулю
- •13. Первообразный корень. Индексы чисел и классов по данному модулю.
- •§2. Первообразные корни
- •§3. Индексы чисел и классов по данному модулю
- •14. Арифметические приложения теории чисел. Теорема Паскаля. Вывод признаков делимости.
- •§2. Признаки делимости
- •§3. Проверка результатов арифметических действий
- •15. Определение длины периода бесконечной десятичной дроби
- •16. Цепные дроби. Существование и единственность значения цепной дроби Представление действительный чисел в виде цепных дробей.
- •17. Подходящие дроби, их свойства.
- •18. Приближение действительных чисел рациональности. Теорема Лагранжа.
- •19. Приближение действительных чисел рациональными дробями
8.Функция Эйлера. Вывод явной формулы для функции Эйлера. Теоремы Эйлера и Ферма.
§ 4. Функция Эйлера
Рассмотрим некоторые свойства функции Эйлера.
1.
Если р - простое, то
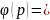 р
-1.
р
-1.
Доказательство.
1,2,3,…, p-1- числа, не превосходящие р и взаимно простые с p. Значит, по определению функции Эйлера, р -1.
2
.

Доказательство.
Идея:
от общего количества натуральных чисел,
не превосходящих
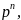 отнимем
количество целых чисел, не взаимно
простых с p.
Числа, не взаимно простые с p,
имеют вид kp,
причем p
отнимем
количество целых чисел, не взаимно
простых с p.
Числа, не взаимно простые с p,
имеют вид kp,
причем p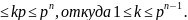 Следовательно,
количество таких чисел ровно
Следовательно,
количество таких чисел ровно
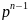 ,
но тогда количество чисел, взаимно
простых с
будет
равно
,
но тогда количество чисел, взаимно
простых с
будет
равно
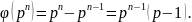
Определение. Функция f(n), определенная на множество натуральных чисел, называется мультипликативной, если для любых взаимно простых натуральных чисел aи b
F(a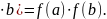
Функция Эйлера мультипликативна, т.е. если (a,b)=1,
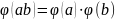 .
.
доказатальство. Натуральные числа от 1 до ab расположим в виде таблицы:
2 … r … b
b+1 b+2 … b+r … 2b
2b+1 2b+2 … 2b+r … 3b
……………………………………………………………
(a-1)b+1 (a-1)b+2 … (a-1)b+r … ab
Подсчитаем это же число другим способом.
Заметим,
что первая строка таблицы есть набор
натуральных чисел, не превосходящих
b,
а значит среди них
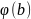 чисел,взаимно простых с b.Но
если число rвзаимнo
просто с b,то
и все числа r-го
столбца взаимно просты с b.Все
числа r-го
столбца сравнимы меду собой по модулю
b,а
сравнимые числа имеют одинаковый НОД
с модулем b.
Следовательно, в таблице
столбцов
чисел, взаимно простых с b.
Пусть r-ый
один из таких столбцов. Он представляет
собой полную систему вычетов по модулю
a
(систему чисел вида bx+r,
где х пробегает полную систему вычетов
по модулю a:
0,1,2, … , a-1).
Но тогда в этом столбце
чисел,взаимно простых с b.Но
если число rвзаимнo
просто с b,то
и все числа r-го
столбца взаимно просты с b.Все
числа r-го
столбца сравнимы меду собой по модулю
b,а
сравнимые числа имеют одинаковый НОД
с модулем b.
Следовательно, в таблице
столбцов
чисел, взаимно простых с b.
Пусть r-ый
один из таких столбцов. Он представляет
собой полную систему вычетов по модулю
a
(систему чисел вида bx+r,
где х пробегает полную систему вычетов
по модулю a:
0,1,2, … , a-1).
Но тогда в этом столбце
 чисел,взаимно простых с а. Если число
взаимно просто с b
и с а, то оно взаимно просто с ab.
Итак, в таблице
столбцов чисел, взаимно простых с b,
каждый такой столбец содержит
чисел,взаимно простых с а. Если число
взаимно просто с b
и с а, то оно взаимно просто с ab.
Итак, в таблице
столбцов чисел, взаимно простых с b,
каждый такой столбец содержит
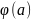 чисел, взаимно простых с а. Значит в
таблице
чисел, взаимно простых с а. Значит в
таблице
 чисел,
взаимно простых как с а, так и с b,
т. е. взаимно простых и с ab. Следовательно,
чисел,
взаимно простых как с а, так и с b,
т. е. взаимно простых и с ab. Следовательно,
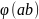 =
=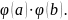
Пусть n=
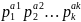 – каноническое раз
– каноническое раз
 ложение
натурального числа, тогда
ложение
натурального числа, тогда
Доказательство.
Т.к. функция Эйлера мультипликативная, то получаем:

Пример.
N=12,
12=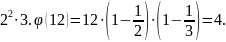
§ 5. Теоремы Эйлера и Ферма
Теорема
Эйлера. Если m>
1 и (а, m)
= 1, то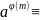 l(mod
m).
l(mod
m).
Доказательство.
Действительно, если x
пробегает приведённую систему вычетов
по модулю m: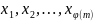 , тогда
ах пробегает тоже
, тогда
ах пробегает тоже
приведённую
систему вычетов:
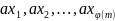 .
.
Поскольку числа приведённой системы вычетов набираются из одних и тех же классов, взаимно простых с модулем, то для каждого числа второй системы найдется сравнимое с ним число первой системы.
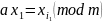

……………

Перемножаем почленно эти сравнения:
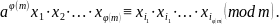
Подчёркнутые произведения состоят из одних и тех же чисел, взаимно простых с модулем. Значит, последнее сравнение можно разделить на подчёркнутое одно и то же число (т.к. оно взаимно просто с модулем). В
результате
получаем
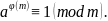
Теорема Ферма. Пусть a Z, р— простое. Если (а,р)=1, то
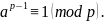
Доказательство следует из теоремы Эйлера при m=р, т.к. р -1.
Следствие.
Для любого целого а и простого p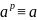 (mod
р).
(mod
р).
Доказательство. 1. Если а не р, то по теореме Ферма
Умножим
обе части сравнения на число а, получим
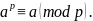
2. Если а р, то a 0(modр) и
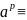 0(mod
р). Следовательно,
0(mod
р). Следовательно,
Пример.
Найти остаток от деления
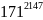 на 52.
на 52.
Решение. Заметим, что число по модулю m сравнимо со своим остатком от деления на m.
1)Заменим
основание степени сравнимым с ним
числом 171
15(mod
52), тогда по свойствам сравнений
 (mod52).
(mod52).
2)Т.к.
(15,52) = 1, то
 =l(mod
52) (теорема Эйлера). Найдем
=l(mod
52) (теорема Эйлера). Найдем
(52)
= 52
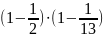 =
24, тогда
=
24, тогда
 = l(mod 52).
= l(mod 52).
3)Разделим 2147 на 24 с остатком:
-
2147
24
192
89
227
216
11
Возведем
обе части сравнения
= l(mod 52) в 89 степень и умножим на
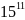 .
Получим
.
Получим
4)Найдем остаток от деления на 52.
 Умножив
на 15, получим
Умножив
на 15, получим
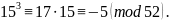 Возведем
обе части в куб:
Возведем
обе части в куб:

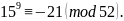 Перемножим
это сравнение и
Перемножим
это сравнение и
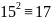 (mod
52) и получим
(mod
52) и получим
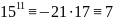 (mod
52).
(mod
52).
тогда
(mod52),
(mod 52),
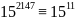 (mod52),
(mod52),
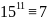 (mod
52). Используя
транзитивное свойство сравнений, видим,
что остаток от делении
на
52 равен 7.
(mod
52). Используя
транзитивное свойство сравнений, видим,
что остаток от делении
на
52 равен 7.
