
- •Отношение делимости. Свойства. Теорема о делении с остатком.
- •Глава 1. Делимость в кольце целых чисел §1. Отношение делимости
- •§2. Теорема о делении с остатком
- •Нод и нок целых чисел. Свойства. Алгоритм Евклида.
- •§3. Нод и нок, алгоритм Евклида
- •Взаимно простые числа. Их свойства. Простые и составные числа. Основное свойство простых чисел.
- •§5. Взаимно простые числа
- •§6. Простые и составные числа Основная теорема арифметики
- •Бесконечность множества простых чисел. Критерий простоты числа. Основное свойство простых чисел
- •§8. Теорема Евклида
- •Основная теорема арифметики и следствия из нее.
- •Сравнения и их свойства.
- •§ 1. Сравнения и их основные свойства.
- •Классы вычитов. Полная и приведенная система вычитов.
- •§ 2. Полная и приведенная система вычетов по модулю m.
- •§ 3. Кольцо классов вычетов.
- •8.Функция Эйлера. Вывод явной формулы для функции Эйлера. Теоремы Эйлера и Ферма.
- •§ 4. Функция Эйлера
- •§ 5. Теоремы Эйлера и Ферма
- •9. Сравнения и системы сравнений с неизвестной величиной.
- •§1. Решение сравнений. Равносильные сравнении
- •§3. Системы сравнений
- •10. Сравнения 1-й степени. Неопределённые уравнения
- •§ 2. Сравнения 1-й степени. Неопределённые уравнения
- •11. Сравнения по простому модулю. Сравнения по степени простого числа. Сравнения по составному модулю.
- •§4 Сравнении с неизвестной величиной по простому модулю
- •§5. Сравнения по составному модулю
- •§6. Сравнения но модулю рn
- •§7. Двучленные сравнения. Квадратичные вычеты и невычеты
- •12. Показатели чисел и классов вычетов по данному модулю
- •§1. Показатели классов и чисел по данному модулю
- •13. Первообразный корень. Индексы чисел и классов по данному модулю.
- •§2. Первообразные корни
- •§3. Индексы чисел и классов по данному модулю
- •14. Арифметические приложения теории чисел. Теорема Паскаля. Вывод признаков делимости.
- •§2. Признаки делимости
- •§3. Проверка результатов арифметических действий
- •15. Определение длины периода бесконечной десятичной дроби
- •16. Цепные дроби. Существование и единственность значения цепной дроби Представление действительный чисел в виде цепных дробей.
- •17. Подходящие дроби, их свойства.
- •18. Приближение действительных чисел рациональности. Теорема Лагранжа.
- •19. Приближение действительных чисел рациональными дробями
Классы вычитов. Полная и приведенная система вычитов.
§ 2. Полная и приведенная система вычетов по модулю m.
Зафиксируем натуральноеm> 1 и рассмотрим произвольное целое число а. Числа, сравнимые с а по модулю m (равноостаточные с а), образуют класс
чисел
по модулю m,
и он обозначается
 .
Класс
.
Класс
 .
Любое число класса называется вычетом
этого класса по модулю m.
Вычет, равный самому остатку, называется
наименьшим
неотрицательным вычетом.
Вычет, самый малый по абсолютной
величине, называется абсолютно
наименьшим вычетом.
.
Любое число класса называется вычетом
этого класса по модулю m.
Вычет, равный самому остатку, называется
наименьшим
неотрицательным вычетом.
Вычет, самый малый по абсолютной
величине, называется абсолютно
наименьшим вычетом.
Определение.Полной системой вычетов по модулюm называется совокупность чисел, взятых по одному из каждого класса вычетов по модулю m.
Пример:
m
= 6. Так как остатки при делении на 6 могут
быть 0,1,2,3.4.5. то по модулю 6 имеется шесть
классов вычетов:
 .
12,7,8, - 3,10,17 - полная система вычетов по
модулю шесть, т.к. 12
.
12,7,8, - 3,10,17 - полная система вычетов по
модулю шесть, т.к. 12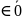 ,7
,7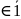 ,8
,8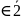 ,
- 3
,
- 3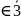 ,10
,10 ,17
,17
0,1,2,3,4,5 -полная система наименьших неотрицательных вычетов, а 0,1,2,3,-2,-1 - полная система абсолютно наименьших вычетов по модулю 6.
Теорема 2 (признак полной системы вычетов). Любая система mчисел, попарно не сравнимых по модулю m, является полной системой вычетов по модулю m.
Доказательство. По условию числа попарно не сравнимы по модулю m, т.е. взяты из разных классов. Т.к. чисел m, то вычет каждого класса присутствует в системе. Значит, это система - полная система вычетов по модулю m.
Теорема 3. Если (а, m)=1 и х пробегает полную систему вычетов по модулю m, то ах+ Ь, где b Z, тоже пробегает полную систему вычетов по модулю m.
Доказательство.
Пусть
х пробегает полную систему вычетов по
модулю m: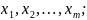 тогда
чисел
тогда
чисел
 тоже
m.
Осталось показать, что эти числа попарно
не сравнимы по модулю m.
Предположим,
что
тоже
m.
Осталось показать, что эти числа попарно
не сравнимы по модулю m.
Предположим,
что
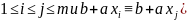 ).
).
Тогда
по свойствам сравнений a = a
= a (modm),
и так как (а,m)=1,
то
(modm),
и так как (а,m)=1,
то
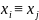 (modm)
(свойство 13); пришли к противоречию.
Следовательно,
(modm)
(свойство 13); пришли к противоречию.
Следовательно,
 +b
принадлежат различным классам. По
признаку имеем полную систему вычетов
по модулю m.
Если (а, m)
= d, то и все числа класса
имеют с m тот же самый НОД (свойство 14
сравнений). Класс чисел
называется
взаимно
простым с модулем m,
если (a, m)=1.
+b
принадлежат различным классам. По
признаку имеем полную систему вычетов
по модулю m.
Если (а, m)
= d, то и все числа класса
имеют с m тот же самый НОД (свойство 14
сравнений). Класс чисел
называется
взаимно
простым с модулем m,
если (a, m)=1.
Определение. Приведённой системой вычетов по модулю m называется совокупность вычетов, взятых по одному из каждого класса, взаимно простого с модулем.
Примеры. 1) 1,2,3,4 - приведенная система вычетов по модулю 5. 2) 1,3, - 3, -1 - приведенная система вычетов по модулю 10.
Определение.
Пусть m
N.
Функцией
Эйлера
называется функция натурального
аргумента
 m),
которая определена как количество
натуральных чисел, не превосходящих m
и взаимно простых с m.
m),
которая определена как количество
натуральных чисел, не превосходящих m
и взаимно простых с m.
Примеры.
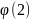 =
1,
=
1,
 (3)=2,
(6)
= 2.
(3)=2,
(6)
= 2.
Заметим,
что в полной системе вычетов по модулю
m:
1,2,3,4,...,mи
ровно
m)
вычетов, взаимно простых с m
(согласно определению
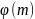 .
.
Теорема 4 (признак приведённой системы вычетов).
Совокупность чисел, попарно не сравнимых по модулю mи взаимно простых с m, образует приведённую систему вычетов по модулю m. Доказательство. Поскольку числа попарно не сравнимы, то они взяты из различных классов. Т.к. они взаимно просты с модулем, то взяты из классов, взаимно простых с модулем. Поскольку их штук, т.е. столько же, сколько классов вычетов взаимно простых с модулем, то вычет каждого такого класса присутствует в системе. Значит, это приведенная система вычетов по модулю m.
Теорема 5. Пусть а Z, m N. Если (а,m) = 1 и в выражении aх переменная х пробегает приведённую систему вычетов по модулю m, то и само выражение ах пробегает приведённую систему вычетов по модулю m.
Доказательство.
Пусть
х пробегает приведённую систему вычетов:
 (1).
Тогда
ах пробегает:
(1).
Тогда
ах пробегает: (2).
Воспользуемся
для системы (2) признаком приведённой
системы вычетов.
(2).
Воспользуемся
для системы (2) признаком приведённой
системы вычетов.
Количество чисел в системе (2) .
Числа попарно не сравнимы по модулю m. В самом деле, пусть i
 j
и a
j
и a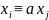 (mod
т). Т.к. (а, m)
= 1, то
(mod
m)
- противоречие с
(mod
т). Т.к. (а, m)
= 1, то
(mod
m)
- противоречие с
тем, что (1) приведенная система вычетов.
3.Т.к (a,m)=1 и ( , m) = 1, то (a ,m) = 1 (свойство взаимно простых чисел). По признаку система (2) - приведенная система вычетов по модулю m.
