Сравнения и их свойства.
§ 1. Сравнения и их основные свойства.
Определение.
Целые числа а и b называются сравнимыми
по модулю m,
если разность а - b делится на m.
Обозначение:
а
b(modm).
Примеры. 5 = -l(mod 6), так как 5-(-1) делится на 6; 1717 37 (mod 10), так как 1717-37 делится на 10; 18 0 (mod 6), так как 18-0 делится на 6.
Теорема 1. Следующие утверждения эквивалентны:
а b(modm), (2) существует t
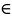Z,
что а=b+
mt (а отличается от b
на число, кратное m),
(3) а и b
при делении на m
дают одинаковые остатки (т.е. а и b
равноостаточные).
Доказательство.
Докажем,
что из (1) следует (2). По определению
имеем: а
b(modm)=>(a-b)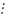
m=>a-b=mt,
t
Z=> а
= b
+ m
t.
Докажем, что из (2) следует (3).Существует
t
Z,
что a = b + mt. Разделим b на mс
остатком, тогда b = mq + r, 0
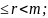а
=mt + mq + r=
m(t + q) + r. Следовательно, а и b имеют
одинаковые остатки.
Докажем,
что из (3) следует (1). а и b при делении на
m
имеют одинаковые остатки: a=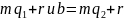
.
Тогда а-b=m(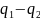
)
m,
т.е.a
b(modm).
Следовательно, данное выше определение
равносильно следующим.
Определение 2. Числа а и b называются сравнимыми по модулю m,если они имеют одинаковые остатки при делении на m.
Определение 3. Числа а и b называются сравнимыми помодулю m, если а от b отличается на число, кратноеm.
Основные свойства сравнений
1. а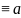
(mod
m)
для любого a
Z
(рефлексивность).
2. Если
a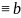
(mod
m),
то b
(mod
m)
(симметричность),
3. Если
a
b(modm)
и b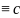
(mod
m),
то a
c(modm)
(транзитивность).
Свойства 1, 2, 3 следуют из того, что сравнимые числа имеют одинаковыетостатки при делении на m.
Из свойств 1-3 вытекает, что отношение сравнимости на множестве целых чисел является отношением эквивалентности.
4 .Если a b(modm), d Z, то а + d b + d(modm), т. e. к обеим частям сравнения можно прибавить одно и то же целое число.
Доказательство.
Если
а
(modm),
то (а-b)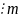
и(а
+ d -(b + d))
;
следовательно, а + d
b
+d(modm).
5. Любое слагаемое сравнения можно переносить в другую часть с противоположным знаком.
Доказательство. Пустьa + b c(modm). Прибавим к обеим частям сравнения - b, получим a с – b(modm).
6. Обе части сравнения можно умножать на одно и то же целое число, т.е. если а b(mod m), то ас c(mod m).
Доказательство. Если a b(modm), то (a-b) m и для любого с Z c(a-b) m.Следовательно
ас c(mod m).
7. Сравнения
по одному и тому же модулю можно почленно
складывать. Доказательство.
а
(mod
m) =>a
+ с
+
c(mod m)
(свойство 4);
с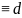
(mod
m)=>b
+ c
b
+ d(m
od
m).
По
3 свойству: a + с
b
+ d(mod
m).
8. Сравнения
по одному и тому же модулю можно почленно
перемножать. Доказательство.
а
(mod
m)=>ас
c(mod
m)
(свойство 6); с
(mod
m)=>bc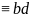
(mod
m).
Тогда по 3 свойству: ас
(mod
m).
9. Обе части сравнения можно возводить в одну и ту же степень с натуральным показателем. Следует из свойства 8.
10. Если
a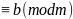
и
f(x)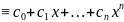
–произвольный
многочлен с целыми коэффициентами,
то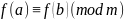
.
Это свойство является следствием
свойств 9,6,7.
11. 
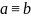(modm),
c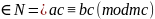
,
т.е. обе части сравнения и модуль можно
умножить на одно и то же натуральное
число.
Доказательство.
Если
(mod
m),то
(a-b)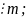
a-b=mt;
ac-bc=mct.
Следовательно, (ac-bc)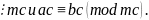
12.
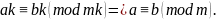Обе части сравнения и модуль можно
разделить на их общий натуральный
делитель.
Доказательство.
Если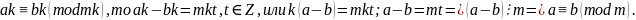
13. Обе части сравнения можно разделить на их общий множитель, если он взаимно прост с модулем.
Доказательство.
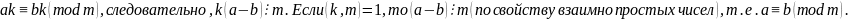
14. Сравнимые
по модулю m
числа имеют один и тот же наибольший
общий делитель с числом m,
т.е. если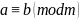
,то
(a,m)=(b,m).
Доказательство.
Т.к.
,
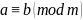то для некоторого
,
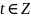a=mt+b.
По лемме к алгоритму Евклида (a,m)=(b,m).
15. Можно
добавлять( или отбрасывать) к любой
части сравнения слагаемые, кратные
модулю. Пусть
.
Т.к. mt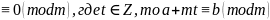
(свойство
7).
16.
=>
.
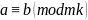Если
,
то a-bделится
на mk,
а значит и на m,
следовательно,
.
17.
Если
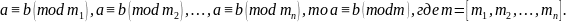
Доказательство.
Так
как
,
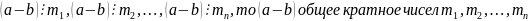и оно делится на НОК этих чисел.
Примеры.
Найти остаток от деления на 11числа
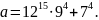
Решение.
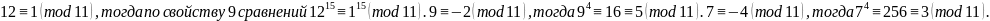Перемножая и складывая соответствующие
сравнения, получим, что
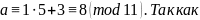а
и 8 при деление на 11 имеют равные остатки(
определение 2), то остаток от деления
на 11 числа а равен 8.
Найти остаток от деления на 6 числа а=
.
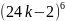Решение.
(24k-2)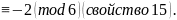
.
.
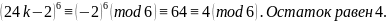
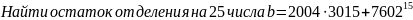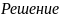2004
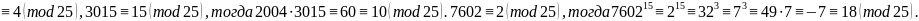Остаток
равен 18.