5. Основная теорема арифметики и следствия из нее.

Теорема (основная теорема арифметики). Любое натуральное число, большее 1, либо является простым, либо может быть представлено в виде произведения простых чисел, причём единственным образом с точностью до порядка сомножителей.

Доказательство. Будем доказывать методом математической индукции. Для п-2 и для простого числа утверждение верно. Единственность представления следует из определения простого числа. Пусть утверждение верно для всех натуральных чисел, больших 1, но меныших п. Докажем справедливость его для числа п. Если п - простое, то утверждение доказано. Если же п - составное, то его можно представить в виде п =ab, где 1< а <п, 1 < b < п. По индуктивному предположению каждое из чисел а и b либо является простым, либо представимо в виде произведения простых чисел. Следовательно, п=ab тоже разлагается в произведение простых чисел.

Докажем единственность представления. Пусть n=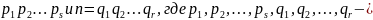 простые числа. Тогда 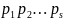= . Так как то (по свойству простых чисел 3) хотя бы один из сомножителей делится на Пусть, например, 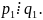Так как оба числа простые, то 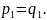После сокращения равенства на получим: Обозначим произведение 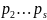= . Так как 1< <n, то по индуктивному предположению s=r, а числа отличаются от чисел порядком. Поэтому при соответствующей нумерации этих чисел = 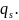Единственность доказана.

Итак, всякое составное число п может быть представлено в виде произведения простых чисел. Среди этих простых множителей могут встречаться одинаковые. Пусть, например,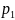 встречается 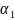раз, встречается 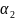раз, ..., встречается раз; тогда разложение числа п на простые множители можно записать следующим образом: n=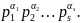

Такое представление числа называют каноническим («канон» по латыни - правило, образец).

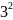Примеры. 60 = * 3 * 5; 81 = ; 666 = 2 * * 37.

Рассмотрим некоторые следствия из основной теоремы.

Следствие 1. Пусть n= каноническое разложение натурального числа п. Все делители п исчерпываются числами вида

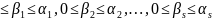n= где 0 (l)

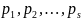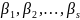Доказательство. Действительно, с одной стороны, всякое число d такого вида делит п. С другой стороны, всякое число, которое делит n, имеет указанный вид, так как по свойствам делимости оно не может иметь других простых сомножителей, кроме , а их показатели не могут противоречить условиям (l).

Заметим, что натуральные числа а и b всегда можно записать в виде a=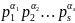 , b= .

Здесь предполагается, что могут принимать и нулевые значения. Это позволит писать в обоих разложениях одни и те же простые числа , а именно простые числа, которые входят в разложение хотя бы одного из чисел а и b. Если числа а и b записаны в указанном виде, то справедливы следующие два утверждения.

Следствие 2. (a, b) = , [a,b]=

Справедливость этих равенств следует из того, что наибольший общий делитель чисел а и b делится на любой их общий делитель, а наименьшее общее кратное чисел а и b делит любое их общее кратное.

Следствие 3. [a,b]*(a,b)=a*b.

Действительно, [a,b]*(a,b)= , где

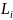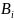Но одно из этих слагаемых равно , а другое - . Следовательно,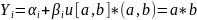 .