Взаимно простые числа. Их свойства. Простые и составные числа. Основное свойство простых чисел.
§5. Взаимно простые числа
Определение. Числа называют взаимно простыми, если наибольший общий делитель этих чисел равен 1.
Примеры. 1) 15, 21, 14 - взаимно простые числа, однако эти числа не являются попарно взаимно простыми.
2) 34, 53, 99, 115 - попарно взаимно простые числа, так как къъшшу простые каждые два числа этого ряда.
Свойства взаимно простых чисел.
1)(Признак взаимно простых чисел) (a, b) =1 тогда и только тогда, когда найдутся целые u и v, что аи + bv = 1.
Доказательство. Необходимость следует из свойства 2 НОД (линейная форма НОД). Докажем достаточность. Пусть d=(a, b). Тогда a⁞d, b⁞ d и au + bv⁞d, то есть l⁞d. Следовательно, d =1.
2)Если (a, b)=1 и (a, с) =1, то (а, bс) = 1.
Доказательство. Воспользуемся признаком. Существуют целые
x,y,
u,
v,
что ах+by=1
и
au + cv =1.
Перемножив эти равенства, получим а(ахи
+ xcv+buy)+bc(yv)
=1,
то есть а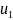
+bc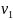
=1
или (а,
bс)=1.
3)Если
ab⁞c
и (a,
с)=1,
то b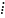
с.
Доказательство. Существуют целые u,v, что au + cv=l. Умножим обе части равенства на b: abu + cbv =b. Так как ab⁞с и c⁞c, то ((ab)u + cbv)⁞ с, то есть b с.
Если a⁞b, a⁞c и (b, с) = 1, то a⁞bc.
Доказательство. Существуют целые u, v, что bu+cv=1.Умножим обе части равенства на а: abu + acv = а. Так как а с, b:b, то
ab⁞bc. Так как а b, с⁞с, то ac⁞bc. Следовательно, (abu + acv)⁞bc и a⁞bc.
§6. Простые и составные числа Основная теорема арифметики
В этом пункте будем рассматривать натуральные числа.
Определение. Натуральное число р называется простым, если р>1 и р не имеет натуральных делителей, отличных от 1 и р.
Определение. Натуральное число п > 1 называется составным, если п имеет по крайней мере один натуральный делитель, отличный от 1 и n.
Пример: 2,3, 5, 7- простые числа, 6, 8,10,15- составные.
1 не является ни простым, ни составным числом. Следовательно, множество натуральных чисел разбивается на 3 класса: простые числа, составные и 1.
Если а - составное число, то из определения следует, что оно имеет натуральный делитель, отличный от 1 и a. Пусть это с. Тогда а = cd. Так как1<с<а,то и 1<d<а.
Свойства простых чисел.
1) Если натуральное число n > 1, то наименьший натуральный делитель его, отличный от 1, — простое число.
Доказательство. Пусть р- наименьший натуральный делитель и, отличный от 1 (п имеет натуральные делители, отличные от 1, например, n). Очевидно, что р - простое число. Иначе оно имело бы такой делитель а, что 1< а < р, но а, будучи делителем р, было бы и делителем п, что противоречит выбору числа р.
2)Если а - целое, р - простое, то а:р или (а,р)=1.
Доказательство. Так как число р имеет только 2 натуральных делителя:
р и 1, то (а,р)= р или (а,р) = 1. В первом случае а⁞р, во втором- а⁞р- взаимно простые числа.
3)(Основное свойство простых чисел.) Если произведение целых чисел ab делится на простое число р, то хотя бы один из сомножителей делится на р.
Доказательство. Пусть аb⁞ р. Если а не делится на р, то (а,р)=1 (свойство2).Тогда по свойству взаимно простых чисел b:р.
Заметим, что свойство может быть распространено на любое конечное число сомножителей.