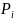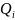18. Приближение действительных чисел рациональности. Теорема Лагранжа.

$4. Квадратичная иррациональность

Определение. Иррациональное число, которое является корнем квадратного уравнения с целыми коэффициентами, называется квадратичной иррациональностью.

Пример: , где n не является квадратом. Квадратичная иррациональность имеет вид 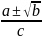(по формуле корней квадратного уравнения), где a,b,c Z, b> 0. Оказывается, квадратичные иррациональности, и только они, разлагаются в бесконечные периодические цепные дроби. Этот замечательный результат был получен впервые в 1770 г. Лагранжем.

Теорема 1. Всякая периодическая цепная дробь изображает квадратичную иррациональность.

Доказательство. Пусть 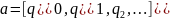-периодическая цепная дробь, т.е. существуют s, к, что

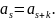
Из равенства (*) (см. § 3) выразим 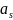через

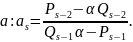
Аналогично Приравняв, получим

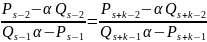
Умножим обе части на общий знаменатель и, приведя подобные, получим квадратное уравнение с целыми коэффициентами вида 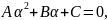где

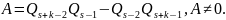
Действительно, если бы 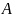=0, то 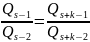. Из свойства (2) подходящих дробей ( )=1. Т.к. две несократимые дроби равны, то

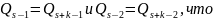
невозможно (т.к. ).

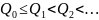Пример. Найти уравнение с целыми коэффициентами, корнем которого является

;

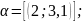
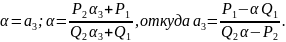
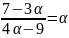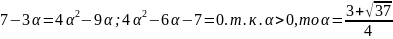
		2	3	1
	1	2	7	9
	0	1	3	4

Теперь докажем, что квадратичная иррациональность разлагается в периодическую цепную дробь.

Лемма. Если =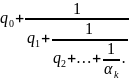 - квадратичная иррациональность, то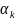 тоже квадратичная иррациональность с тем же дискриминантом (дискриминантом квадратичной иррациональности называют дискриминант квадратного уравнения, корнем которого является квадратичная иррациональность).

Доказательство. Пусть α- корень уравнения

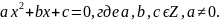
Подставим вместо x

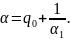
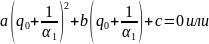
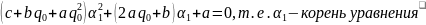
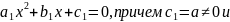
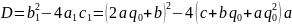
где D- дискриминант исходного уравнения.

Подставим в уравнение 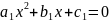вместо x 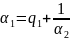, получим аналогично, что - корень квадратного уравнения с тем же дискриминантом и т.д.

Теорема Лагранжа. Любая квадратичная иррациональность разлагается в периодическую цепную дробью

Без доказательства!

19. Приближение действительных чисел рациональными дробями

На практике обычно приходится заменять иррациональное число рациональным, мало отличающимся от него числом. При этом стараются выбрать рациональное число возможно простым, т.е. в виде десятичной дроби с небольшим числом знаков после запятой или в виде обыкновенной дроби со сравнительно небольшим знаменатилем. Иногда и громоздкие рациональные числа приходится заменять их приближениями.

Цепные дроби – удобный аппарат для приближений. Мы знаем, что, если 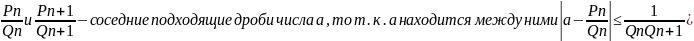_n+1). Действительно, 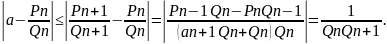Или более грубая оценка 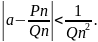Вообще говоря, подходящие дробидают лучшее приближение к числу, чем десятичные: 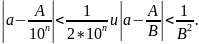Возникает вопрос, можно ли найти такое приближение a рациональной дробью, чтобы точность была во много раз больше, чем величина, обратная знаменателю, например: 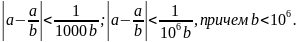Оказывается можно.

Теорема Дирихле. Для любого действительного числа а и произвольного τ>1 можно найти рациональную дробь

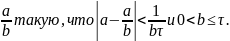
Доказательство. Пусть 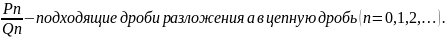Найдем наибольший номер n, чтобы Q_{n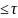 ,} и в качестве дроби

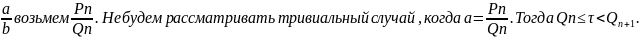
Следствие (из теоремы Дирихле). Всякое простое число вида p=4k+1 равно сумме двух квадратов.

5=1+2², 17=1²+4² и т.д.

Доказательство. Если p=4k+1, то (-1) является квадратичным вычетом по модулю p (свойство символа Лежандра), т.е. существует m, m²≡-1(mod p). Возьмем

Если y=mx-pz, то |y|<

Подходящие дроби в определенном смысле являются лучшими приближениями к действительному числу. А именно, рациональную дробь считают наилучшим приближением к числу а, если не существует рациональных дробей со знаменателем меньшим или равным b, которые бы находились к а ближе чем . Иначе говоря, в интервале 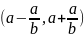любая рациональная дробь будет иметь знаменатель больше b. А дробь со знаменателем меньшим либо равным b будет лежать за пределами этого интервала.

Теорема. При s≥1 любая подходящая дробь 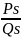к действительному числу а являются наилучшим приближением.

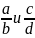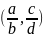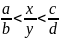Доказательство. Сначала докажем, что если рациональные дроби таковы, что bc-ad=1, то любая рациональная дробь в интервале имеет знаменатель больший, чем b и d. То есть если , то y>b и y>d.

Пусть

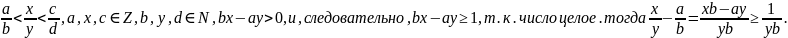
С другой стороны,

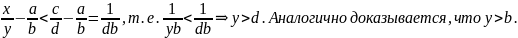
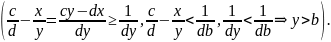
Т.к. а лежит между