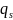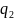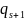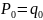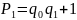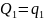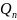17. Подходящие дроби, их свойства.

Пусть – конечная или бесконечная цепная дробь.

Определение 1. Дроб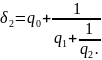и , , и т.д.

Называются соответственно нулевой, первой и т.д.

k-ой подходящими дробями цепной дроби или соответствующего ей числа α.

Очевидно, что если α - рациональное число, то последняя подходящая дробь 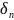есть число α.

Каждая подходящая дробь есть некоторое рациональное число. Поставим задачу найти общую формулу для вычисления подходящей дроби любого порядка.

Заметим, что s-я подходящая дробь 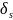получается путем замены

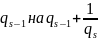
Рассмотрим выражение вида , где необязательно целые числа, и рассмотрим две последовательности чисел: , определенных рекуррентными соотношениями:

(6)

Теорема. Выражение , где s 0, равно

Доказательство. Докажем методом математической индукции. Для s=0,1,2 еаходим непосредственно

=

=

= = =

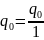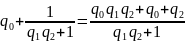Предположим, что утверждение верно для n, т.е.

= .

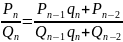Подставим в обе части равенства вместо 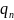выражение .

=

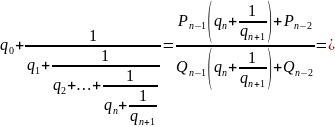
Теорема доказана.

Вернемся снова к цепным дробям. Мы получили хороший способ для вычисления подходящих дробей. По теореме n-я подходящая дробь равна , где вычисляются по рекуррентным формулам, причем - целые.

Вычисления по формулам удобно проводить с помощью таблицы:

s		0	1	2	…	s	s+1	…	n
					…			…
	1				…		…	…
	0				…		…	…

Например, для получения нужно стоящее над ним число умножить на стоящее слева от клетки для число и к результату прибавить стоящее слева от число .

Аналогично вычисляется и .

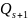Замечание. Числа 1 и 0 поставлены во втором столбце с тем, чтобы это правило можно было применять и к вычислению и

Пример 1. Разложим в непрерывную дробь число и найдем все подходящие дроби разложения.

С помощью алгоритма Евклида получаем:

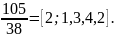
0

Подходящие дроби находим по схеме:

s		0	1	2	3	4
		2	1	3	4	2
	1	2	3	11	47	105
	0	1	1	4	17	38

Последовательные подходящие дроби:

, , .

Основные свойства подходящих дробей

1) Числители и знаменатели подходящих дробей — целые числа; знаменатели, кроме того, числа натуральные и образуют возрастающую последовательность.

Доказательство. Первое утверждение очевидно, так как q( — числа целые.

Докажем второе. Действительно,

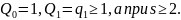
, где . Значит,

2) Числители и знаменатели двух соседних подходящих дробейmсвязаны соотношением:

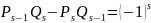(7)

Доказательство. Используем метод математической индукции.

а) При s=1 имеем: 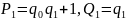и ( , т.е. при s=1 соотношение (7) имеет место.

b) Предположим верность формулы (7) для s=k: и докажем верность ее для s=k+1.

+ =- = ,

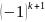Итак, .

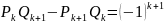Тогда согласно принципу математической индукции формула (7) верна для любого натурального s.

3) Подходящие дроби несократимы, т. е. ( , ) = 1.

Доказательство. Действительно, согласно свойству 2) подходящих дробей имеем: =

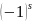
Если допустить, что ( , )≠1, т. е. что ( , ) = d >1, то из равенства (7)

следует, что делится на d > 1 , что невозможно. Следовательно, ( , ) = 1.

Замечание. Если рациональное число , разложить в цепную дробь, то последняя подходящая дробь , в этом разложении несократима и равна .

Таким образом, разложение в цепную дробь позволяет сокращать дроби.

4) Подходящие дроби с четными номерами образуют возрастающую, а с нечетными—убывающую последовательность.

Доказательство. Пользуясь формулами (6) и (7), получим:

Итак,

Если k- четное, то , или

т.е. подходящие дроби с четными номерами образуют возрастающую последовательность.

Если k- нечетное, то , или

т.е. подходящие дроби с нечетными номерами образуют убывающую последовательность.

5)Каждая подходящая дробь с четным номером 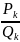меньше соседних подходящих дробей

Доказательство. Используя свойство 2 подходящих дробей, находим:

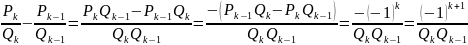
Заменяя k на k+1, получим:

Если k- четно, то 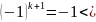0, а =1 > 0. Значит, при четном k

Это и показывает, что

Следствие. Каждая подходящая дробь с нечетным номером больше соседних подходящих дробей

6) Любая подходящая дробь с четным номером меньше любой подходящей дроби с нечетным номером.

Доказательство. На основании четвертого и пятого свойств при k получаем: <

При k получаем: <

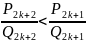
Следовательно, при любых соотношениях между l и k выполняется неравенство: 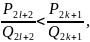которое доказывает свойство 6.

7) Если t — положительное рациональное число, то при его разложении в цепную дробь подходящие дроби с четными номерами — приближение по недостатку; а с нечетными — по избытку (за исключением последней дроби, совпадающей с t)

Доказательство. Если последняя подходящая дробь, совпадающая с числом t имеет четный номер, то она (по свойству 4) больше остальных подходящих дробей с четными номерами, которые дают, таким образом, приближения t по недостатку. Вместе с тем число t как подходящая дробь с четным номером меньше любой подходящей дроби с нечетным номером (по свойству 6), а потому подходящие дроби с нечетными номерами дают для t приближение с избытком. Аналогично рассматривается случай, когда последняя подходящая дробь, совпадающая с t, является дробью с нечетным номером (читателю рекомендуется рассмотреть этот случай самостоятельно).

8) Если t – положительное рациональное число и k-я подходящая дробь в разложении t в непрерывную дробь, то

(8)

Доказательство. Так как на основании свойства 7 число t заключено между любыми двумя своими соседними подходящими дробями, то

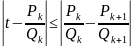(9)

Но (10)

(см. доказательство свойства 5).

Тогда из (9) и (10) следует:

Так как при k>1, , то а потому .

Следовательно

Пример. Заменим число такой подходящей дробью, чтобы полученная при этом погрешность не превышала 0,001.

Решение. Разлагаем данное число в цепную дробь:

Получим:

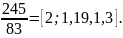
Находим подходящие дроби:

s		0	1	2	3	4
		2	1	19	1	3
	1	2	3	59	62	245
	0	1	1	20	21	83

Следовательно, дробь

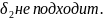
Ответ. Искомая подходящая дробь .

3.Бесконечные цепные дроби

Пусть 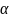- иррациональное число

Этот процесс можно продолжать без конца. На некотором этапе имеем 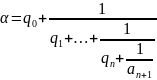4

(*)

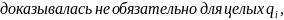
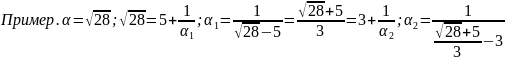
Теорема. Бесконечная последовательность подходящих дробей, которая возникает при описанном выше разложении иррационального числа в цепную дробь, сходится к .

Доказательство. Из (*)

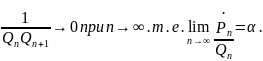
Замечание. Из доказательства теоремы следует, что если заменить подходящей дробью , то погрешность меньше .

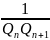Итак, иррациональное число может быть представлено бесконечной цепной дробью. Возникает вопрос. Если взять произвольную бесконечную цепную дробь, то можно ли ей придать какое-либо значение?

Теорема. Если из бесконечной последовательности чисел 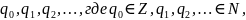образовать бесконечную цепную дробь, то соответствующая последовательность подходящих дробей имеет предел.

Доказательство. Т.к. последовательность подходящих дробей с четными номерами возрастает, а с нечетными убывает и любая подходящая дробь с четным номером меньше любой подходящей с нечетным номером, то подходящие дроби с четными и нечетными номерами являются концами последовательности вложенных друг в друга отрезков длины которых стремится к нулю при

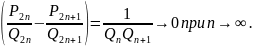
Получаем стягивающуюся последовательность отрезков, имеющих единственную общую точку, которая является пределом последовательности как левых, так и правых концов отрезков. Таким образом, бесконечной цепной дроби мы можем придать значение . Из доказательства видно, что ( если -рациональное, то совпадает с последней подходящей дробью.)

Теорема. Представление действительного иррационального числа цепной дробью единственно.

Иначе говоря, можно утверждать, что представление действительного иррационального числа в виде бесконечной непрерывной дроби всегда является разложением с помощью выделения цепной части.

Докажем это важное утверждение.

Доказательство. Пусть действительное иррациональное представлено бесконечной непрерывной дробью Так как любая бесконечная цепная дробь представляет некоторое действительное число,то это утверждение относится так же и к цепной дроби Аналогично, 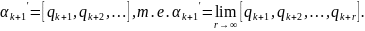В силу этого из соотношения предельным переходом получаем

. (.)

.к. при

.

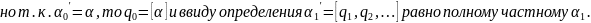
Элементы данной бесконечной непрерывной дроби получаются, таким образом, из его значения последовательным выделением целой части; это и требовалось доказать.

Итак, мы получили следующий основной результат: каждое иррациональное действительное число единственным образом представляется бесконечной непрерывной дробью вида , и наоборот, каждой бесконечной цепной дроби соответствует единственное иррациональное действительное число, которое она представляет.