16. Цепные дроби. Существование и единственность значения цепной дроби Представление действительный чисел в виде цепных дробей.

$1. Понятие цепной дроби

Любое рациональное число t можно записать в виде

Представим число t в виде дроби особого вида. Это представление тесно связано с алгоритмом Евклида. Применим алгоритм Евклида к числам a и b; последовательно получим:

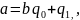
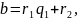
(1)

………………………………

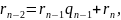
где , причем так как .

Равенство (1) можно записать в следующем виде:

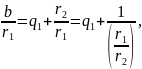
(2)

………………………….

Заменяя последовательно каждую из дробей и т.д. ее соответствующим выражением из следующей строки, получим представление дроби в виде

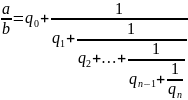
Определение 1. Выражение вида

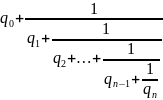(3)

Где , , называется конечной цепной или непрерывной дробью.

Числа называются как и в алгоритме Евклида неполными частными или элементами цепной дроби. Сокращенно цепную дробь будем обозначать: ].

Если =с – целое, то цепная дробь имеет вид [c].

Нами доказана следующая теорема:

Теорема 1. Всякое рациональное число может быть представлено в виде конечной цепной дроби.

Примеры.

1)

37=15*2+7,

15=7*2+1,

7=1*7,

2)

13=141*0+13

141=13*10+11

13=11*1+2

11=2*5+1

2=1*2

3)

-43=15*(-3)+2

15=2*7+1

2=2*1

Следовательно,

4)

5)

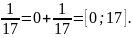
6)9=[9]

7)-19=[-19]

Требование существенно для однозначной записи числа в виде цепной дроби.

Если допустить, что последнее неполное частное может равняться 1, то для всякого рационального числа можно получить два представления в виде конечной цепной дроби.

Пример.

2+

Теорема 2. Представление рационального числа в виде непрерывной дроби единственно.

Доказательство (от противного). Пусть возможны два представления числа

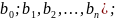=[ =[ (4)

Тогда =

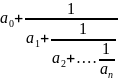Рассмотрим второе слагаемое левой части равенства, обозначив его через c

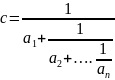
Здесь все – натуральные.

Если n>1, то

Если n=1, то т.к. >1, то и в этом случае т.е. с – всегда правильная дробь.

Тогда = .

Аналогично: = .

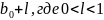Это значит, что 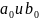— целые части одного и того же числа . Но так как целая часть числа определяется однозначно, то .

После вычитания из обеих частей (4) получим равные дроби с равными числителями, но тогда и знаменатели этих дробей равны, т. е.

=

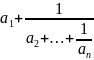Рассуждая аналогично, получим последовательно: 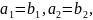и т.д. Далее возможны три случая:

1)n=k; 2) n<k; 3) n>k.

1-й случай. n=k. Тогда

Теорема доказана.

2-й случай. n<k. Тогда получим

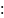
, (5)

где 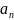— целое число, а правая часть равенства (5) - число дробное.

Значит, случай n < к невозможен.

Аналогично доказывается невозможность и случая n > к. Остается первый случай: . Теорема доказана.

Теорема 3. Всякая конечная цепная дробь есть рациональное число.

Доказательство. Пусть дана цепная дробь (3). Если произвести указанные арифметические действия над целыми числами 1 и 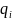то получим рациональное число.

При доказательстве теоремы 2 получен другой способ разложения в цепную дробь, а именно - выделение целой части и обращение (переворачивание) дробной.

Пример.

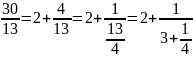
Этот метод можно применить и к иррациональному числу .

Пример. – дробная часть числа a 1- целая. Из равенства найдем = ;

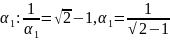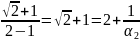. Так как 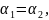то, начиная с этого момента, неполные частные будут повторяться, т.е. Получим бесконечную периодическую цепную дробь (бесконечная цепная дробь, в которой последовательность непарных частных, начиная с некоторого момента, повторяется, называется периодической).

Определение 2. Выражение вида 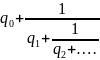, где называется бесконечной цепной дробью, а числа - ее элементами или неполными частными.