§7. Двучленные сравнения. Квадратичные вычеты и невычеты

Двучленные сравнения - сравнения вида axⁿ≡b(mod m). (l)

Если (a,m)= 1, то сравнение (1) можно привести к еще более простому виду. Взяв с такое, что ас ≡ l(mod m), и умножив обе части сравнения (1) на с (оно взаимно просто с m), получим хⁿ≡bс(mod m). Будем рассматривать сравнения такого вида по простому модулю р, отличному от 2, то есть сравнения вида x² ≡ a(mod р). (2)

Теорема 1. Сравнение 2-ой степени ax²+bx+c≡0(mod p), где р - простое, р > 2, может быть сведено к двучленному сравнению (2).

Доказательство. Действительно, умножим обе части сравнения на 4a (взаимно простое с модулем). Имеем 4a²x² + 4abx +4ac≡0(mod p),

(2ax + b)² ≡-4ас + b²(mod р). Обозначив 2ax+b= у, b² -4aс = d, получим у² ≡ d(mod р).

Примеры. 1.

Решить сравнение Зх² + 7x+ 8 ≡0(mod 17).

36х² + 12*7х+ 12*8 ≡ 0(modl7), (6х + 7)² ≡49-96(mod 17), (6х + 7)² ≡ -47 + 5l(mod l7), (6х + 7)² ≡4(mod l7), (6x+7)≡±2(mod17).

6x≡-5 +17(mod 17), x≡ 2(mod 17) или 6x ≡ -9(mod17), 2x≡ -3 +17(mod 17), x ≡ 7(mod 17).

Ответ: x ≡ 2(mod 17), x ≡ 7(mod 17).

Это Сравнение можно было привести к двучленному, заменив коэффициенты сравнимыми с ними числами и используя другие свойства

сравнений. Зх² +24x-9 ≡ 0(mod l7) (здесь вместо 7 взяли 24, а вместо 8 число -9), х² +.8х-3 ≡ 0(mod 17), (х + 4)² ≡ 19 +17(mod 17),

(Х + 4) ≡ ±6(mod 17).

2.Решить сравнение 4x² — 1 1х — 3 ≡ 0(mod 13).

4х² -24х + 36 ≡0(mod l3), х² -6х + 9 ≡ 0(mod 13), (х -З)² ≡ 0(mod 13), х-3 ≡0(mod 13), x≡3(mod 13).

Если в сравнении хⁿ ≡a(mod p) а делится на р, то и х делится на р и х ≡ 0(mod р) - единственное решение сравнения.

Пусть а не делится на р.

Определение. Число а называют n-степенным вычетом или n-степенным невычетом по модулю р в зависимости от того, имеет или нет решение сравнение хⁿ ≡ a(mod р), где (а, р) = 1.

В частности, число а называют квадратичным вычетом или квадратичным невычетом по модулю р в зависимости от того, имеет или

нет решение сравнение х² ≡ a(mod p), где (а, р) = 1. Если а - квадратичный вычет (невычет) по модулю р, то и любое число из класса а также является квадратичным вычетом (невычетом), поэтому квадратичным вычетом (невычетом) можно называть класс по модулю р.

Пример.

Выяснить, является ли квадратичным вычетом по модулю 5 число 3. Проверим, имеет ли решение сравнение х² ≡3(mod 5) .

Взяв приведённую систему вычетов по модулю 5: ±1, ±2, убеждаемся, что сравнение не имеет решений, то есть 3 - квадратичный невычет, а квадратичными вычетами будут 1 и 4.

Легко видно, что если сравнение (2) имеет решение х ≡x0(mod р), то оно также имеет решение х ≡-x0(mod р). При р >2 классы х0 и - х0 - разные классы. Действительно, если бы х0 ≡ -x0(mod р), то 2х0 ≡ 0(mod р), чего быть не может, так как ни 2, ни x0 не делятся на р. Сравнение (2) не может иметь более чем 2 решения, как сравнение 2-ой степени по простому модулю. Итак, нами доказана следующая теорема.

Теорема 2. Если (a,р) =1 , р - простое, р> 2, то сравнение х² ≡a(mod р) либо не имеет решений, либо имеет два решения.

Для нахождения решений сравнения х² ≡ a(mod р) можно взять приведённую систему вычетов, наименьших по абсолютной величине, по

модулю р: ± 1,±2,...,± 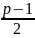. Более того, достаточно проверить лишь числа 1,2,..., (p-1)/2. При подстановке этих чисел в сравнение (2) в левой части сравнения получаются числа 1,2²,…,(p-1/2)². Если одно из них, например, k² сравнимо с а по модулю р, то получим решения сравнения (2): x≡±k(mod p). Мы видим, что сравнение (2) имеет решения лишь для тех чисел а, которые сравнимы с одним из чисел

1,22,…,(p-1/2)2 (3)

по модулю р, то есть в ряду (3) записаны представители всех классов квадратичных вычетов по модулю р. Причём числа (3) принадлежат разным классам по модулю р. Действительно, если для 1≤k<l≤(p-1)/2. k² ≡l² (mod р), то сравнение (2) имело бы 4 решения: ±k,±l, что невозможно. Итак, имеем (p-1)/2 классов квадратичных вычетов и столько же классов квадратичных невычетов (так как всего p-1 классов, взаимно простых с модулем). Нами доказана теорема.

Теорема 3. Число классов квадратичных вычетов по простому модулю р, р> 2, равно числу классов квадратичных невычетов, ровно (р-1)/2.

Пример.

Найдём наименьшие неотрицательные квадратичные вычеты по модулю 13. Их должно быть (p-1)/2=6. Ими являются числа: 1,2² =4,3² = 9, 4² ≡3(mod l3), 5² ≡12(mod 13), 6²≡10(mod 13), то есть 1,3,4, 9, 10, 12. Оставшиеся от приведённой системы вычетов числа: 2,5, 6, 7, 8,11 - квадратичные невычеты. Рассмотренный способ недостаточно эффективен для установления разрешимости сравнения (2). Рассмотрим другой способ.

Критерий Эйлера. Число а является квадратичным вычетом по простому модулю р (р > 2, (а,р)=1) тогда и только тогда, когда a^(p-1)/2≡1(mod p) и квадратичным невычетом тогда и только тогда, когда a^(p-1)/2≡-1(mod p).

Доказательство.

По т. Ферма a^p-1≡1(mod p), то есть a^p-1-1 делится на р или (a^(p-1)/2-1)(a^(p-1)/2+1) делится на р. Оба сомножителя не могут делиться на р, иначе их разность, равняя 2, делилась бы на р, что невозможно. Если а - квадратичный вычет, то а ^(p-1)/2 -1 делится на р. Действительно, существует х0, (х0,р) = 1, что х0² ≡a(modр), Т0ГДа a^(p-1)/2≡(x0²)^(p-1)/2≡x0^p-1≡1(mod p). То есть a^(p-1)/2 ≡1(mod p)Итак, любой

квадратичный вычет удовлетворяет сравнению х^(p-1)/2 ≡ l(mod p) (4)

и вычетов (p-1)/2. Следовательно, это сравнение имеет не менее чем(p-1)/2 решений. Но и не более, так как сравнение по простому модулю имеет решений не больше, чем его степень. Поэтому квадратичные вычеты, и только они, удовлетворяют сравнению (4). Тогда для остальных а, (а,р)=1, то есть для квадратичных невычетов, и только для них, второй сомножитель делится на р, то есть a^(p-1)/2≡-1(mod p).

Пример.

Выяснить, сколько решений имеет сравнение х² ≡7(modl9). (p-1)/2=9. Проверим, будет ли 7⁹ сравнимо с 1 по модулю 19. 7² ≡-8(modl9), 7³ ≡l(modl9), 7⁹ ≡l(mod 19). Следовательно, 7 - квадратичный вычет и сравнение имеет 2 решения.