§5. Сравнения по составному модулю

Теорема. Если m = р1^a1 p2^a2 …..ps^as - каноническое разложение числа m, то сравнение f(x) ≡ 0(mod m), (1), равносильно системе

(2)

Доказательство.

Если х0 удовлетворяет сравнению (1), то х0 удовлетворяет и системе (2) (если f(x0):m, то f(xo ):рi^ai ). Обратно, если х0 удовлетворяет системе (2), то по 17-му свойству сравнений х0 удовлетворяет сравнению по модулю, равному НОК чисел р1^a1,р2^a2,...,рs^as : f(x)≡0(mod [p1^a1 ,р2^a2 ,...,рs^as ]),то есть f(x) ≡ 0(mod m).

Для нахождения решений системы (2) обычно решают каждое сравнение системы. Если при этом хотя бы одно сравнение не имеет решений, то система (2) и сравнение (1) не имеют решений, если же каждое сравнение системы имеет решение, то система (2) может быть представлена в виде

(3)

Эта система имеет одно решение – класс по модулю m, так как модули сравнений системы попарно взаимно просты. Если некоторые из сравнений системы (2) имеют более одного решения, то получим несколько систем вида (3).

Пример:

X²-3x+23≡0(mod 63). Сравнение равносильно системе

решения первого сравнения: классы 1,2; второго: классы -1,4.

Следовательно, сравнение равносильно совокупности четырех систем:

Каждая система имеет одно решение, так как 7 и 9 взаимно просты. Найдем их. Умножая обе части и модуль первого сравнения каждой системы на 9, а второго на 7, имеем:

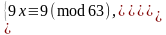
Вычтем из первого сравнения второе, получим соответственно: 2x≡16(mod 63), 2x≡-19(mod 63), 2x≡25(mod 63), 2x≡-10(mod 63), откуда

x≡8(mod 63), x≡22(mod 63), x≡44(mod 63), x≡-5(mod 63).

§6. Сравнения но модулю рn

Решение сравнения по составному модулю, как доказано в предыдущем пункте, сводится к решению сравнений вида f(x) ≡0(mod pⁿ).| Решать такие сравнения методом подбора, очевидно, очень неудобно. Поэтому весьма примечательно то, что решение сравнения по модулю pⁿ , где р - простое и n> 1, может быть сведено к решению сравнения модулю р.

Рассмотрим сравнение f(x) ≡0(mod рⁿ) (1),

Где f(x)€Z[x], p- простое и n>1. Если x0 удовлетворяет сравнению (1),то оно удовлетворяет сравнению f(x)≡0(mod p) (2). Поэтому среди чисел, удовлетворяющих сравнению(2), будем искать те, которые удовлетворяют сравнению f(x)≡0(mod p²), среди них те, которые удовлетворяют сравнению f(x)≡0(mod p³), и так далее, пока не получим решения сравнения (1). Итак, пусть найдено одно решение сравнения (2): х≡x1(mod p), или х = х1 + pt, t€ Z. Будем искать такие t, чтобы f(x1+pt)≡0(mod p²). (3) Заменим многочлен f(x1+pt) его разложением но формуле Тейлора

+

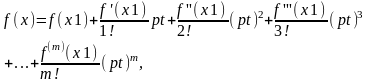где. как известно, все коэффициенты - числа целые. Так как в правой части равенства все слагаемые, кроме первых двух, делится на p²,то сравнение (3) равносильно сравнению f(x1)+f’(x1)pt≡0(mod p²) или f’(x1)pt≡-f(x1)(mod p²). f(x1):p (x1 удовлетворяет сравнению (2)), поэтому разделим обе части сравнении и модуль на p: f’(x1)t≡- (4)

Рассмотрим случай, когда f’(x1) не делится на р, то есть (f’(x1),p)=1. Тогда сравнение 1-ой степени (4) имеет одно решение t≡t1(mod p) или t=t1+pk, k€Z. Подставим найденное t в выражение для х: x=x1+ pt1 + р²k и обозначим x1+pt1 через x2. X2 удовлетворяет

Сравнению f(x)≡0(mod p²), то есть x=x2+p²k – решение этого сравнения. Будем искать такие k, чтобы f(x2+p²k)≡0(mod p³). (5)

Опять заменим многочлен f(x2+p²k) его разложением по формуле Тейлора

Так как все слагаемые, кроме первых двух, делятся на p³, то сравнение (5) равносильно сравнению f(x2)+f’(x2)p²k≡0(mod p³) или так как f(x2):p², f’(x2)k≡- (6)

Поскольку x2≡x1(mod p), то f’(x2)≡f’(x1)(mod p). Но f’(x1) не делится на р, следовательно, f’(x2) не делится на р и сравнение (6) имеет одно решение k=k1+pl, l€Z. При помощи найденного решения составим решение сравнения f(x)≡0(mod p³) x=x2+k1p²+lp³ или

X=x3+lp³. И так далее, пока не получим решение сравнение (1). Итак, нами доказана следующая теорема.

Теорема. Если f’(x1) не делится на р, то каждое решение класса x1 сравнения f(х) ≡ 0(mod р) приводит к одному решению сравнения

f(x) ≡ o(mod рⁿ).

Вернёмся к сравнению (4) и рассмотрим теперь случай, когда f'(х1) делится на р, а правая часть сравнения не делится на р (класс х1 - решение сравнения (2)). Тогда сравнение не разрешимо, вместе с тем неразрешимо будет также f(x)≡0(mod р²) и (l) не имеет решений в классе х1.

Если же правая часть (4) делится на р, то t - любое целое и все числа х = х1 + pt удовлетворяют сравнению f(х)≡ 0(mod p²), но по модулю р² они уже но будут принадлежать одному классу, так как класс х1 по модулю р разбивается на р классов по модулю р² :

X1, x1+p, x1+2p,…, x1+(p-1)p

Пример 1.

Х³ - 2х² - 3Ох + 41 ≡ 0(mod 125),

f(x) = х³ - 2х² - ЗОх + 41, f'(x)= Зх² - 4х- 30. Решаем сравнение по модулю 5. Х³ - 2х² - ЗОх + 41≡0(mod 5) равносильно сравнению

х³ - 2х² +1 ≡ 0(mod5). Взяв полную систему вычетов по модулю 5, находим решения: классы 1, -2.

1. Рассмотрим класс 1. Среди чисел вида х = 1 + 5t будем искать те, что удовлетворяют сравнению f(l + 5t) ≡0(mod 5² ), которое равносильно сравнению f(l) + f'(1)5t ≡0(mod 5²). Имеем 10 — 31*5t ≡ 0(mod 25), 2-31t≡0(mod 5), t≡2(mod 5), t = 2 + 5k,

х = 1+ 5(2 + 5k)= 11 + 25k, x≡1 l(mod 25). Далее решаем сравнение f(l 1 + 25k) ≡0(mod 5³), равносильное сравнению f(11)+f’(11)25k≡0(mod 5³).

f(l l) = 121* 11-242-330 + 41 ≡-4*11+ 8 +45 + 41 ≡ 50(modl25),

f'(11)≡ -12 - 44 - 30 ≡ 39(mod 125) . 50+39 • 25 k≡ 0(mod 125)

2+39k ≡0(mod5); k ≡2(mod 5); k = 2 + 5l; x = 11 + 25(2 + 5l)=61 + 125l. Получили решение исходного сравнения х ≡ 6l(mod 125)

2. Проделаем то же самое с числами вида х = -2 + 5t из класса -2.f(- 2 + 5t) ≡0(mod 5²), f(- 2) +f'(- 2)5t≡0(mod 52)

85 - 10 • 5t ≡ 0(mod 25) Это сравнение решений не имеет.

Ответ: х ≡ 6 l(mod 125)

Пример 2.

2х² –х-1≡0(mod27). f(x)=2x²-x-1, f’(x)=4x-1.

2х²-х-1 ≡0(mod 3), класс 1 - решение этого равнения, x=1+3t, t€Z.

f(l)+f'(l)*3t ≡ 0(mod9), 0 + 3*3t≡0(mod 9), откуда t - любое число, то есть все числа вида x=l+3t, t€Z, удовлетворяет последнему сравнению. Однако класс 1 по модулю 3 разбивается на классы 1,4,7 по модулю 9, Рассмотрим числа этих классов.

1. х = 1+9k, 0 + 3*9k≡0(mod 27), k – любое. Класс 1 по модулю 9 разбивается на 3 класса по модулю 27: 1,10,19.

2. X=4+9k, f(4)+f’(4)*9k≡0(mod 27), 27+15*9k≡0(mod 27). K – любое. Получаем решения по модулю 27: 4,13,22.

3. X=7+9k, f(7)+f’(7)*9k≡0(mod 27), 90+27*9k≡0(mod 27).

Сравнение решений не имеет.

Ответ: х ≡ 1 (mod 27), х ≡10(mod 27), x≡19(mod 27), x≡4(mod 27), x≡13(mod 27), x≡22(mod 27).

Короче: x≡ 1 + 9k(mod27), х≡4 + 9k(mod27), где k равно 0,1,2.