
- •Вопрос 1. Аксиомы поля. Поле комплексных чисел. Запись комплексного числа.
- •1)Коммутативность сложения и умножения.
- •2)Умножения
- •3)Ассоциативность
- •Вопрос 2.Кольцо матриц над полем действительных чисел. Основные операции над матрицами. Свойства операций.
- •Сложение (вычитание) матриц – складывать (вычитать) по элементам и только над матрицами одинаковой размерности.
- •Умножение матрицы на число , произведение.
- •Коммуникативность:
- •Ассоциативность:
- •Вопрос 3. Определители. Теорема Лапласа. Свойства определителей.
- •Теорема лапласа. (Метод рекурентных соотношений)
- •Вопрос 4. Обратная матрица. Метод присоединенной матрицы и метод элементарных преобразований.
- •Вопрос 5. Теорема о Ранге матрице.
- •Вопрос 6. Теорема Кронекера-Капелли
- •Достаточность
- •Вопрос 7. Решение слу. Метод Крамера, матричный метод, метод Гауса
- •Если система (2.3) имеет единственное решение, определяемое по формулам: .
- •Вопрос 8.Однородные слу. Построение фундаментальной системы решений
- •Вопрос 9. Векторы. Основные понятия. Скалярное произведение, его свойства
- •Вопрос 10. Векторное произведение векторов. Свойства.
- •Вопрос 11. Смешанное произведение. Свойства
- •Вопрос 12. Преобразование координат на плоскости. Парралельный перенос. Поворот.
- •Вопрос 13. Кривые второго порядка.Каноническое уравнение эллипса.
- •Эллипс.
- •Вопрос 14. Кривые второго порядка.Каноническое уравнение параболы и гиперболы.
- •Парабола.
- •Вопрос 15. Классификация кривых 2-го порядка.Приведение к каноническому виду. Кривая второго порядка может быть задана уравнением
- •Вопрос 16. Плоскость в пространстве. Основные типы уравнений плоскости.
- •Для того, чтобы через три какие- либо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой.
- •Пусть заданы точки м1(x1, y1, z1), m2(x2, y2, z2) и вектор .
- •Пусть заданы два вектора и , коллинеарные плоскости. Тогда для произвольной точки м(х, у, z), принадлежащей плоскости, векторы должны быть компланарны.
- •Вопрос 17. Прямая в пространстве. Основные типы уравнений.
- •Уравнение прямой в пространстве, проходящей
- •Вопрос 18. Метод сечений в пространстве.Эллипсоиды и гиперболоиды.(с примерами).
- •Цилиндрические поверхности.
- •Гиперболоид.
- •Вопрос 19. Метод сечений.Цилиндры и Конусы.(с примерами).
- •Цилиндр
- •Вопрос 20. Линейные пространства.Основные понятия.Теорема о Базисе.
- •Вопрос 21. Матрица перехода от Базиса к Базису.
- •Вопрос 22. Линейный оператор и его матрица.
- •Вопрос 23. Собственные значения и собственные векторы линейных операторов.
- •Вопрос 24.Приведение уравнения 2-го порядка к каноническому виду(Алгоритм, с примером).
- •Вопрос 25.Множество операций над множеством.
- •Операции над множествами.
- •Вопрос 26.Докозательсво , что множество действительных числе не .
- •Вопрос 27. Функция, последовательность, их пределы (примеры бесконечно малых и больших последовательностей).
- •Вопрос 28. Теорема о пределе монотонной ограниченной последовательности, теорема о пределе промежуточной функции.
- •Вопрос 32.Неопределенности.Сравнение бесконечно малых. Таблица эквивалентности.
Вопрос 13. Кривые второго порядка.Каноническое уравнение эллипса.
 Кривой
2-го порядка наз-ся множество точек в
декартовой плоскости, которая удовлетворяет
уравнению следущего вида:
Кривой
2-го порядка наз-ся множество точек в
декартовой плоскости, которая удовлетворяет
уравнению следущего вида:
Ах2 + 2Вху + Су2 + 2Dx + 2Ey + F = 0.
Существует система координат (не обязательно декартова прямоугольная), в которой данное уравнение может быть представлено в одном из видов, приведенных ниже.
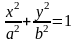 -
уравнение эллипса.
-
уравнение эллипса.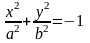 -
уравнение “мнимого”
эллипса.
-
уравнение “мнимого”
эллипса.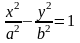 -
уравнение гиперболы.
-
уравнение гиперболы.y2 = 2px – уравнение параболы.
y2 – a2 = 0 – уравнение двух параллельных прямых.
y2 + a2 = 0 – уравнение двух “мнимых” параллельных прямых.
y2 = 0 – пара совпадающих прямых.
(x – a)2 + (y – b)2 = R2 – уравнение окружности.
Эллипс.
 Определение.
Эллипсом в каноническом виде наз-ся
множество всех точек плоскости координаты
которых удовлетворяют уравнению
.
Определение.
Эллипсом в каноническом виде наз-ся
множество всех точек плоскости координаты
которых удовлетворяют уравнению
.
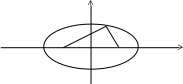
Определение. Фокусами называются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина.
M
М
r1
r2
F1
O
F2

r1
М
r1
r2
F1
O
F2
r2
М
r1
r2
F1
O
F2
O
М
r1
r2
F1
O
F2
x
М
r1
r2
F1
O
F2
F2
М
r1
r2
F1
O
F2
F1
М
r1
r2
F1
O
F2
F1, F2 – фокусы. F1 = (c; 0); F2(-c; 0)
с – половина расстояния между фокусами;
a – большая полуось;
b – малая полуось.
Теорема. Фокусное расстояние и полуоси эллипса связаны соотношением:
a2 = b2 + c2.
откуда
c=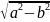
 Определение.
Форма эллипса определяется характеристикой,
которая является отношением фокусного
расстояния к большей оси и называется
эксцентриситетом.
Определение.
Форма эллипса определяется характеристикой,
которая является отношением фокусного
расстояния к большей оси и называется
эксцентриситетом.
Е = с/a.
Т.к. с < a, то е < 1.
Теорема. Для произвольной точки М(х, у), принадлежащей эллипсу верны соотношения:
 r1
= a
– ex,
r2
= a
+ ex.
r1
= a
– ex,
r2
= a
+ ex.
Доказательство. Выше было показано, что r1 + r2 = 2a. Кроме того, из геометрических соображений можно записать:
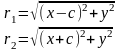
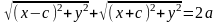
После возведения в квадрат и приведения подобных слагаемых:
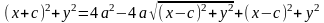
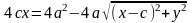
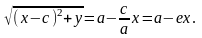
Аналогично доказывается, что r2 = a + ex. Теорема доказана.
С эллипсом связаны две прямые, называемые директрисами. Их уравнения:

x = a/e; x = -a/e.
Отношение расстояния ri от точки эллипса до фокуса Fi к расстоянию di от этой точки до отвечающей фокусу директрисы равно эксцентриситету эллипса.
Доказательство.
Расстояния от точки М(х, у) до фокусов эллипса можно представить так:
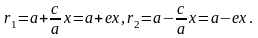 Составим уравнения
директрис:
Составим уравнения
директрис:
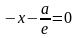 (D1),
(D1),
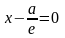 (D2).
Тогда
(D2).
Тогда
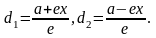 Отсюда ri
/ di
= e,
что и требовалось доказать.
Отсюда ri
/ di
= e,
что и требовалось доказать.
Теорема 2:
т.
М принадлежит эллипсу
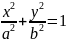 не являющемуся окружностью, тогда и
только тогда, когда отношение расстояния
от М до фокуса к расстоянию от М до
соответствующей этому фокусу директриссы
равно эксцентриситету.
не являющемуся окружностью, тогда и
только тогда, когда отношение расстояния
от М до фокуса к расстоянию от М до
соответствующей этому фокусу директриссы
равно эксцентриситету.
Доказательство:
Обозначим
через l (L-малая)
директриссу
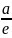 ,
расстояние от точки М (х,у) до данной
директриссы равно
,
расстояние от точки М (х,у) до данной
директриссы равно
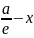 ,
преобразуем
,
преобразуем
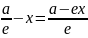 ,
используя лемму получаем, что если
точка М принадлежит эллипсу, то
,
используя лемму получаем, что если
точка М принадлежит эллипсу, то
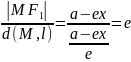
Достаточность пусть М(х,у) произвольная точка в плоскости, для которой выполняется:
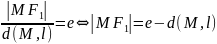 по
формулам длины отрезка:
по
формулам длины отрезка:
 ,
,
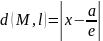 возведем
данное уравнение в квадрат:
возведем
данное уравнение в квадрат:
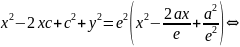
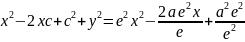
зная что ea=c, последнее равенство будет выглнядеть:
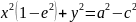 ,
так как
,
так как
 , а
, а
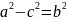 в итоге получим:
в итоге получим:
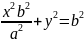
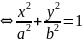 таким
образом точка М принадлежит эллипсу.
таким
образом точка М принадлежит эллипсу.
